《2025年拔尖特训九年级数学上册苏科版》

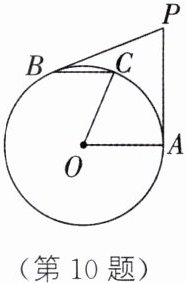
10. 如图,PA、PB是⊙O的切线,A、B为切点,C为$\overset{\frown}{AB}$上的一点,∠AOC= ∠P.
(1)求证：BC//AO.
(2)若BC= 10,AO= 13,求PA的长.
]

答案：
(1)如图，连接BO,延长AO交⊙O于点D.
∵PA、PB是⊙O的切线,A、B为切点，
∴∠OBP=∠OAP=90°.
∴∠P+∠AOB=180°.
∵∠AOB+∠BOD=180°,
∴∠BOD=∠P.
∵∠AOC=∠P,
∴∠AOC=∠BOD.
∴∠COB+2∠AOC=180°.
∵OC=OB,
∴∠BCO=∠CBO.
∴∠COB+2∠BCO=180°.
∴∠AOC=∠BCO.
∴BC//AO.
(2)如图,延长BC交PA于点E,过点O作OF⊥BC于点F.
∴BF=CF=$\frac{1}{2}$BC=$\frac{1}{2}$×10 = 5.
∵CO=AO=13,
∴在Rt△COF中,FO= $\sqrt{CO² - CF²}$ = 12.
由
(1),知∠OAP=90°,BC//AO,
∴∠AEF=180° - ∠OAP=90°,
又
∵FO⊥BC,即∠OFE=90°,
∴四边形AOFE是矩形.
∴AE=FO=12,EF=AO=13.
∵PA、PB是⊙O的切线，A、B为切点，
∴PA=PB.
设PA=PB=x,则PE=x - 12.
∵∠AEF=90°,
∴∠PEB=90°.
∵BE=BF+EF=5+13=18,在Rt△BPE中,由勾股定理,得PB² = PE² + BE²,
∴x²=(x - 12)²+18²,解得x = $\frac{39}{2}$.
∴PA = $\frac{39}{2}$.

11. 如图,AB为⊙O的直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证：OQ= PQ.
(2)连接BC并延长,交PQ于点D,PA= AB,且CQ= 6,求BD的长.
]

答案：
(1)如图，连接OP.
∵PA、PC分别与⊙O相切于点A、C,
∴PA=PC,OA⊥PA,OC⊥PC.
∵OA=OC,OP=OP,
∴△OPA≌△OPC.
∴∠AOP=∠COP.
∵PQ⊥PA,
∴PQ//AB.
∴∠QPO=∠AOP.
∴∠COP=∠QPO.
∴OQ=PQ.
(2)设OA=r,则PA=PC=AB=2r.
∵OB=OC,
∴∠OBC=∠OCB.
由
(1),得PQ//AB,
∴∠QDC=∠OBC.
∵∠OCB=∠QCD,
∴∠QCD=∠QDC.
∴CQ=QD=6.
∵OQ=PQ,
∴OQ - QC=PQ - QD,即OC=PD=r.
∴PQ=QD+PD=6+r.
∵PC是⊙O的切线,
∴OC⊥PC.
∴∠OCP=∠PCQ=90°.
在Rt△PCQ中,由勾股定理,得PQ²=PC²+CQ²,即(6+r)²=(2r)²+6²,解得r=4或r=0(不合题意，舍去).
∴OA=4,AP=8.
∴在Rt△AOP中,OP= $\sqrt{OA² + AP²}$ = 4$\sqrt{5}$.
∵OC=PD,OB=OC,
∴OB=PD.
又
∵PQ//AB,即OB//PD,
∴四边形OBDP是平行四边形.
∴BD=OP=4$\sqrt{5}$.

12. ★新考法·探究题【探究问题】
(1)如图①,PM、PN、EF分别切⊙O于点A、B、C,猜想△PEF的周长与切线长PA之间的数量关系并证明.
△PEF的周长=2PA.
∵PA、PB分别切⊙O于点A、B,
∴PA=PB.
∵PA、EF分别切⊙O于点A、C,
∴EA=EC.
同理,可得FC=FB.
∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF=PE+EA+FB+PF=PA+PB=2PA.
【变式迁移】
(2)如果(1)中的条件不变,且点P到点O的距离为10 cm,△PEF的周长为16 cm,那么⊙O的半径为______cm.
6
【拓展提高】
如图②,E是∠MPN的边PM上一点,EF⊥PN于点F,⊙O与边EF及射线PM、射线PN都相切.
(3)画出符合条件的⊙O.
如图①②,⊙O即为所求作.
(4)若EF= 3,PF= 4,求⊙O的半径.
如图①,设⊙O分别与射线PM、射线PN、边EF相切于点A、B、C,连接OA、OB、OC.
∴AE=CE,∠OBF=90°,∠OCF=90°.
∵EF⊥PN,
∴∠CFB=90°.
∴四边形OCFB为矩形.
又
∵OC=OB,
∴四边形OCFB为正方形.
∴CF=BF=OC.
设⊙O的半径为r,则CF=BF=r.
∵在Rt△PEF中,EF=3,PF=4,
∴PE= $\sqrt{PF² + EF²}$ = 5,AE=CE=3 - r.
∵PA=PB,
∴PE+AE=PF+BF,即5+3 - r=4+r,解得r=2.
∴⊙O的半径为2.
如图②,设⊙O的半径为R.
∵EF⊥PN,
∴∠EFP=90°.
∵在Rt△PEF中,EF=3,PF=4,
∴PE= $\sqrt{PF² + EF²}$ = 5.
∵易得S△PEF = $\frac{1}{2}$(EF + PF + PE)·R = $\frac{1}{2}$EF·PF,
∴$\frac{1}{2}$×(3 + 4 + 5)R = $\frac{1}{2}$×3×4,解得R = 1.
∴⊙O的半径为1.
综上所述,⊙O的半径为2或1.

答案：
(1)△PEF的周长=2PA.
∵PA、PB分别切⊙O于点A、B,
∴PA=PB.
∵PA、EF分别切⊙O于点A、C,
∴EA=EC.
同理,可得FC=FB.
∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF=PE+EA+FB+PF=PA+PB=2PA.
(2)6.
(3)如图①②,⊙O即为所求作.
(4)如图①,设⊙O分别与射线PM、射线PN、边EF相切于点A、B、C,连接OA、OB、OC.
∴AE=CE,∠OBF=90°,∠OCF=90°.
∵EF⊥PN,
∴∠CFB=90°.
∴四边形OCFB为矩形.
又
∵OC=OB,
∴四边形OCFB为正方形.
∴CF=BF=OC.
设⊙O的半径为r,则CF=BF=r.
∵在Rt△PEF中,EF=3,PF=4,
∴PE= $\sqrt{PF² + EF²}$ = 5,AE=CE=3 - r.
∵PA=PB,
∴PE+AE=PF+BF,即5+3 - r=4+r,解得r=2.
∴⊙O的半径为2.
如图②,设⊙O的半径为R.
∵EF⊥PN,
∴∠EFP=90°.
∵在Rt△PEF中,EF=3,PF=4,
∴PE= $\sqrt{PF² + EF²}$ = 5.
∵易得S△PEF = $\frac{1}{2}$(EF + PF + PE)·R = $\frac{1}{2}$EF·PF,
∴$\frac{1}{2}$×(3 + 4 + 5)R = $\frac{1}{2}$×3×4,解得R = 1.
∴⊙O的半径为1.
综上所述,⊙O的半径为2或1.