《2025年拔尖特训九年级数学上册苏科版》

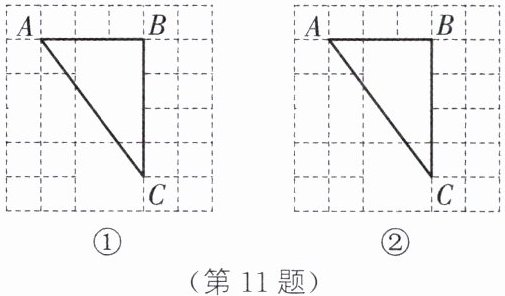
11. 如图①②,在6×6的正方形网格中,有部分网格线被擦去,点A、B、C在格点(正方形网格的交点)上.
(1)请用无刻度的直尺在图①中找到△ABC的外心P.
(2)请用无刻度的直尺在图②中找到△ABC的内心Q.

答案： （1）如图①，点P即为所求作.
（2）如图②，点Q即为所求作.

12. ★如图,在等腰三角形ABC中,AC= BC,AD是边BC上的高,⊙E是△ACD的内切圆,分别与边AD、CD、AC相切于点F、G、I.
(1)求证：AF= BG.
(2)过点E作EH⊥AB于点H,试探究EH与AB之间的数量关系,并说明理由.
答案讲解

答案： （1）如图，连接AE、CE、IE、GE、EF.
∵⊙E是△ACD的内切圆，
∴∠ICE = ∠GCE，∠CIE = ∠CGE = 90°.
又
∵CE = CE，
∴△CIE≌△CGE.
∴CI = CG.
同理，可得AI = AF.
∵AC = BC，CI = CG，
∴AC - CI = BC - CG，即AI = BG.
∴AF = BG.
（2）$EH=\frac{1}{2}AB$.
理由:如图，连接BE.
在△ACE和△BCE中，
$\begin{cases} AC=BC, \\ ∠ACE=∠BCE, \\ CE=CE, \end{cases}$
∴△ACE≌△BCE.
∴∠AEC = ∠BEC，AE = BE.
∵⊙E是△ACD的内切圆，
∴∠ACE = ∠DCE = $\frac{1}{2}$∠ACD，∠CAE = ∠FAE = $\frac{1}{2}$∠CAD.
∴∠AEC = 180° - （∠ACE + ∠CAE） = 180° - $\frac{1}{2}$（∠ACD + ∠CAD）.
∵∠ACD + ∠CAD = 180° - ∠ADC，∠ADC = 90°，
∴∠AEC = 180° - $\frac{1}{2}×(180° - 90°)$ = 135°.
∴∠BEC = 135°.
∴∠AEB = 360° - ∠AEC - ∠BEC = 90°.
又
∵AE = BE，
∴△ABE为等腰直角三角形.
∵EH⊥AB，
∴AH = BH，即H为AB的中点.
∴$EH=\frac{1}{2}AB$.

13. 到三角形的两边距离相等的点,叫做此三角形的“准内心”.如图①,PD⊥AB,PE⊥BC.若PD= PE,则点P为△ABC的“准内心”.
(1)如图②,BF为等边三角形ABC的角平分线,△ABC的“准内心”P在BF上,PD⊥AB,PE⊥BC,且$PF= \frac{1}{2}BP.$求证：点P是△ABC的内心.
(2)如图③,△ABC为直角三角形,∠C= 90°,△ABC的“准内心”P在AC上,PD⊥AB.若$PC= \frac{1}{2}AP,$求∠A的度数.
答案讲解

答案： （1）
∵△ABC是等边三角形，
∴∠ABC = 60°.
∵BF为等边三角形ABC的角平分线，
∴∠PBE = $\frac{1}{2}$∠ABC = 30°，BF⊥AC.
又
∵PE⊥BC，即∠PEB = 90°，
∴易得$PE=\frac{1}{2}BP$.
∵$PF=\frac{1}{2}BP$，
∴PE = PF.
∵点P为△ABC的“准内心”，PD⊥AB，PE⊥BC，
∴PD = PE.
∴PE = PD = PF.
∴点P是△ABC的内心.
（2）
∵△ABC的“准内心”P在AC上，PD⊥AB，∠C = 90°，
∴PD = PC.
又
∵$PC=\frac{1}{2}AP$，
∴$PD=\frac{1}{2}AP$.
∴易得∠A = 30°.