《2025年拔尖特训九年级数学上册苏科版》

10. 如图,AB是⊙O的直径,C是$\overset{\frown}{AB}$的中点,点D在$\overset{\frown}{BC}$上,BD、AC的延长线交于点K,连接AD、BC交于点E,连接CD.
(1)求证：∠AKB－∠BCD＝45°.
(2)若CD＝$\sqrt{2}$BD,求证：BC＝2CK.
 

答案：
（1）
∵ AB是⊙O的直径，
∴ ∠ACB=∠ADB=90°.
∵ C是$\overset{\frown}{AB}$的中点，
∴ AC=BC.
∴ △ABC是等腰直角三角形.
∴ ∠CAB=∠CBA=45°.
∵ $\overset{\frown}{CD}=\overset{\frown}{CD}$,$\overset{\frown}{BD}=\overset{\frown}{BD}$，
∴ ∠DAC=∠CBK，∠DAB=∠BCD.设∠DAC=∠CBK=α,则∠DAB=∠BCD=45°-α,∠AKB=90°-α.
∴ ∠AKB-∠BCD=(90°-α)-(45°-α)=45°.（2）如图,过点C作CH⊥AD于点H.
∴ ∠CHD=90°=∠ADB.
∵ ∠CDH=∠CBA=45°，
∴ 易得△CHD是等腰直角三角形.
∴ 易得CD=$\sqrt{2}$CH.
∵ CD=$\sqrt{2}$BD，
∴ CH=BD.在△ECH和△EBD中，$\left\{\begin{array}{l} ∠CEH=∠BED,\\ ∠CHE=∠BDE,\\ CH=BD,\end{array}\right.$
∴ △ECH≌△EBD.
∴ CE=BE.
∴ CE=$\frac{1}{2}$BC.
∵ AB是⊙O的直径，
∴ ∠ACE=90°.
∴ ∠BCK=90°.
∴ ∠ACE=∠BCK.在△ACE和△BCK中，$\left\{\begin{array}{l} ∠CAE=∠CBK,\\ AC=BC,\\ ∠ACE=∠BCK,\end{array}\right.$
∴ △ACE≌△BCK.
∴ CE=CK.
∴ CK=CE=$\frac{1}{2}$BC.
∴ BC=2CK.

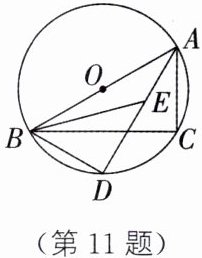
11. 如图,以AB为直径的⊙O经过△ABC的顶点C,AE、BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)试判断△BDE的形状,并证明你的结论.
(2)若AB＝10,BE＝$2\sqrt{10}$,求BC的长.

答案：
（1）△BDE为等腰直角三角形.
∵ AE平分∠BAC,BE平分∠ABC，
∴ ∠BAE=∠CAD=∠CBD，∠ABE=∠EBC.
∵ ∠BED=∠BAE+∠ABE，∠DBE=∠DBC+∠CBE，
∴ ∠BED=∠DBE.
∴ BD=ED.
∵ AB为⊙O的直径，
∴ ∠ADB=90°.
∴ △BDE是等腰直角三角形.（2）如图,连接OC、CD、OD,OD交BC于点F.
∵ ∠DBC=∠CAD=∠BAD=∠BCD，
∴ BD=DC.
∵ OB=OC，
∴ OD垂直平分BC.
∴ BC=2BF.
∵ △BDE是等腰直角三角形,BE=2$\sqrt{10}$，
∴ 易得BD=2$\sqrt{5}$.
∵ AB=10，
∴ OB=OD=5.设OF=t,则DF=5-t.在Rt△BOF和Rt△BDF中,BF²=OB²-OF²,BF²=BD²-DF²，
∴ 5²-t²=(2$\sqrt{5}$)²-(5-t)²,解得t=3.
∴ BF=$\sqrt{OB^2-OF^2}=4$.
∴ BC=8.

12. 如图①,⊙M交x轴于B、C两点,交y轴的正半轴于点A,点M的纵坐标为2,点B、C的坐标分别为$(-3\sqrt{3},0)$、$(\sqrt{3},0)$.
(1)求⊙M的半径.
(2)如图②,若CE⊥AB于点H,交y轴于点F,求证：EH＝FH.
(3)在(2)的条件下,求AF的长.
 

答案：
（1）如图①,过点M作MT⊥BC于点T,连接BM.
∵ BC是⊙M的一条弦,MT⊥BC，BC=3$\sqrt{3}+\sqrt{3}=4\sqrt{3}$，
∴ BT=TC=$\frac{1}{2}$BC=2$\sqrt{3}$.
∴ BM=$\sqrt{BT^2+MT^2}=\sqrt{12+4}=4$,即⊙M的半径为4.（2）如图②,连接AE,则∠AEC=∠ABC.
∵ CE⊥AB，
∴ ∠AHE=∠AHF=90°.
∴ ∠HBC+∠BCH=90°.在△COF中，
∵ 易得∠OFC+∠OCF=90°，
∴ ∠AEH=∠HBC=∠OFC=∠AFH.在△AEH和△AFH中，$\left\{\begin{array}{l} ∠AEH=∠AFH,\\ ∠AHE=∠AHF,\\ AH=AH,\end{array}\right.$
∴ △AEH≌△AFH.
∴ EH=FH.（3）如图③,作直径BG,连接AC、CG、CM,过点M作MT⊥BC于点T,由（1）,易知∠BMT=∠BAC=60°,则∠BGC=∠BAC=60°.
∵ MC=MG，
∴ △MCG是等边三角形.
∴ CG=CM=4.连接AG,
∵ ∠BCG=90°，
∴ CG⊥x轴.
∴ CG//AF.
∵ ∠BAG=90°，
∴ AG⊥AB.
∵ CE⊥AB，
∴ AG//CE.
∴ 四边形AFCG为平行四边形.
∴ AF=CG=4.