第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 如图,点O是△ABC的内心,也是△DBC的外心.若∠A= 84°,则∠D的度数为(
A.42°
B.66°
C.76°
D.82°
B
)A.42°
B.66°
C.76°
D.82°
答案:
B
2. (2023·聊城)如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB、IA.若∠CAI= 35°,则∠OBC的度数为(
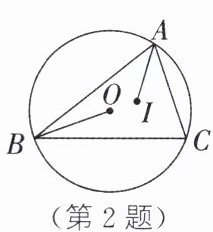
A.15°
B.17.5°
C.20°
D.25°
C
)
A.15°
B.17.5°
C.20°
D.25°
答案:
C
3. (2024·苏州期末)如图,△ABC的周长是18 cm,⊙O是△ABC的内切圆,过点O作EF//AB,与AC、BC分别交于点E、F.已知AB= 6 cm,则△CEF的周长为

12
cm.
答案:
12
4. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,点E在AD的延长线上,∠CDE= 78°,则∠AIC的度数为
129°
.
答案:
129°
5. (2024·镇江一模)如图,等腰三角形ABC内接于⊙O,AB= AC,点I是△ABC的内心,连接BI并延长,交⊙O于点D,点E在BD的延长线上,满足∠EAD= ∠CAD.求证:
(1)OA所在的直线经过点I.
(2)D是IE的中点.
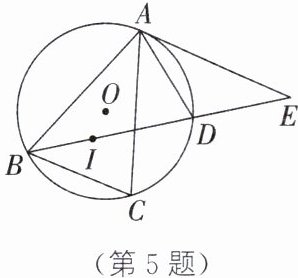
(1)OA所在的直线经过点I.
(2)D是IE的中点.

答案:
(1)如图,连接OA、OB、OC、AI.
∵AB = AC,OB = OC,OA = OA,
∴△AOB≌△AOC.
∴∠BAO = ∠CAO.
∴AO平分∠BAC.
∵点I是△ABC的内心,
∴AI平分∠BAC.
∴AO与AI在同一条直线上.
∴OA所在的直线经过点I.
(2)如图,连接OD,则OD = OA.
∴∠OAD = ∠ODA.
∴2∠OAD + ∠AOD = 180°.
∴∠OAD + $\frac{1}{2}$∠AOD = 90°.
∵∠ABD = $\frac{1}{2}$∠AOD,
∴∠OAD + ∠ABD = 90°.
∵点I是△ABC的内心,
∴∠ABD = ∠CBD.
∴∠ABD = ∠CBD = ∠CAD = ∠EAD.
∴∠IAE = ∠OAD + ∠EAD = 90°.
∵∠DIA = ∠ABD + ∠BAO = ∠CAD + ∠CAO = ∠DAI,
∴ID = AD.
∵∠DIA + ∠E = 90°,∠DAI + ∠DAE = 90°,
∴∠E = ∠DAE.
∴ED = AD.
∴ID = ED.
∴D是IE的中点.
∵AB = AC,OB = OC,OA = OA,
∴△AOB≌△AOC.
∴∠BAO = ∠CAO.
∴AO平分∠BAC.
∵点I是△ABC的内心,
∴AI平分∠BAC.
∴AO与AI在同一条直线上.
∴OA所在的直线经过点I.
(2)如图,连接OD,则OD = OA.
∴∠OAD = ∠ODA.
∴2∠OAD + ∠AOD = 180°.
∴∠OAD + $\frac{1}{2}$∠AOD = 90°.
∵∠ABD = $\frac{1}{2}$∠AOD,
∴∠OAD + ∠ABD = 90°.
∵点I是△ABC的内心,
∴∠ABD = ∠CBD.
∴∠ABD = ∠CBD = ∠CAD = ∠EAD.
∴∠IAE = ∠OAD + ∠EAD = 90°.
∵∠DIA = ∠ABD + ∠BAO = ∠CAD + ∠CAO = ∠DAI,
∴ID = AD.
∵∠DIA + ∠E = 90°,∠DAI + ∠DAE = 90°,
∴∠E = ∠DAE.
∴ED = AD.
∴ID = ED.
∴D是IE的中点.
6. 新考向·数学文化(2024·滨州)刘徽(今山东滨州人)是魏晋时期伟大的数学家,我国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,在Rt△ABC中,∠C= 90°,AB、BC、CA的长分别为c、a、b,则可以用含c、a、b的式子表示出△ABC的内切圆直径d,下列表达式中,错误的是
D
答案:
D
7. 已知△ABC的外心为点O,内心为点I,∠BOC= 120°,则∠BIC的度数为(
A.120°
B.130°
C.120°或150°
D.130°或150°
C
)A.120°
B.130°
C.120°或150°
D.130°或150°
答案:
C 解析:如图①,当∠A是锐角时,
∵点O为△ABC的外心,∠BOC = 120°,
∴易得∠A = 60°.
∴∠ABC + ∠ACB = 120°.
∵点I为△ABC的内心,
∴∠IBC + ∠ICB = 60°.
∴∠BIC = 120°.如图②,当∠A是钝角时,
∵∠BOC = 120°,
∴易得∠A = 120°.
∴∠ABC + ∠ACB = 60°.
∵点I为△ABC的内心,
∴∠IBC + ∠ICB = 30°.
∴∠BIC = 150°.综上所述,∠BIC的度数为120°或150°.
∵点O为△ABC的外心,∠BOC = 120°,
∴易得∠A = 60°.
∴∠ABC + ∠ACB = 120°.
∵点I为△ABC的内心,
∴∠IBC + ∠ICB = 60°.
∴∠BIC = 120°.如图②,当∠A是钝角时,
∵∠BOC = 120°,
∴易得∠A = 120°.
∴∠ABC + ∠ACB = 60°.
∵点I为△ABC的内心,
∴∠IBC + ∠ICB = 30°.
∴∠BIC = 150°.综上所述,∠BIC的度数为120°或150°.
8. 如图,点I为△ABC的内心,连接AI并延长,交△ABC的外接圆于点D,AI= 2CD,E为AC的中点,连接EI、IC.若IC= 6,ID= 5,则IE的长为______
4
.
答案:
4
9. (2024·无锡梁溪期末)如图,在Rt△ABC中,∠C= 90°,AC= 5,BC= 12,AM= 1,点I为△ABC的内心,连接IM,则IM的长为______

$2\sqrt{2}$
.
答案:
$2\sqrt{2}$
10. 如图所示的网格由边长为1个单位长度的小正方形组成,点A、B、C在平面直角坐标系中的坐标分别为(3,6)、(-3,3)、(7,-2),则△ABC内心的坐标为
(2,3)
.
答案:
(2,3)
查看更多完整答案,请扫码查看


