《2025年拔尖特训九年级数学上册苏科版》

1. P是⊙O外一点,PA、PB分别切⊙O于点A、B,∠P= 70°,C是⊙O上的点(不与点A、B重合),则∠ACB的度数为 (D)
A.70°
B.55°
C.70°或110°
D.55°或125°

答案： D

2. 在⊙O中,AD是直径,∠DAB= 31°,C是⊙O上的一动点(不与点A、B重合),则∠ACB的度数为 (D)
A.31°
B.59°
C.31°或59°
D.59°或121°

答案： D

3. 已知圆中的一条弦所对的圆心角是30°,则这条弦所对的圆周角的度数是15°或165°.

答案： 15°或165°

4. 如图,⊙O的半径为2,AB是⊙O的弦,P是弦AB上的一动点,且$\sqrt{2}\leqslant OP\leqslant 2$,则弦AB所对的圆周角的度数为______.

答案：
45°或135° 解析:如图,连接OA、OB,过点O作OD⊥AB于点D,在⊙O上AB的两侧分别取点E、F,连接AE、BE、AF、BF.
∵ P是弦AB上的一动点,且√2≤OP≤2,
∴ OD = √2.
∴ AD = √(OA² - OD²) = √2.
∴ AD = OD.
∴ ∠OAB = ∠AOD = 45°.
∵ OA = OB,OD⊥AB,
∴ ∠AOD = ∠BOD.
∴ ∠AOB = 2∠AOD = 90°.
∴ ∠AEB = 1/2∠AOB = 45°.
∵ ∠E + ∠F = 180°,
∴ ∠F = 135°.综上所述,弦AB所对的圆周角的度数为45°或135°.
　　　　　

6. 如图,在□OABC中,以点O为圆心、OC长为半径的圆切AB于点B,F是圆上一动点,作射线AF交⊙O于另一点E.当EF= BC时,∠BAF的度数为______.

答案：
75°或15° 解析:如图,当AF在OA的上方时,连接OE、OF、OB,过点O作OH⊥EF于点H.
∵ OE = OB,OF = OC,EF = BC,
∴ △OEF≌△OBC.
∴ 易得∠C = ∠OBC = ∠E = ∠OFE.
∵ 以OC长为半径的圆切AB于点B,
∴ OB⊥AB.
∵ 四边形OABC是平行四边形,
∴ OA = BC,AB//OC.
∴ OB⊥OC.
∴ △OBC是等腰直角三角形.
∴ 易得∠C = ∠OAB = ∠OBC = 45°.
∴ ∠E = ∠EFO = 45°.
∴ 易得OH = 1/2EF.
∵ OA = BC = EF,
∴ OH = 1/2OA.
∴ 易得∠OAH = 30°.
∴ ∠BAF = 45° + 30° = 75°.当AF(即AF')在OA的下方时,同理,可得∠OAF' = 30°.
∴ ∠BAF' = 45° - 30° = 15°.综上所述,∠BAF的度数为75°或15°.
　　　　

7. 如图,在⊙O中,AD为直径,弦BC⊥AD于点H,连接OB.已知OB= 2 cm,∠OBC= 30°,动点E在直径AD上从点D向点A以1 cm/s的速度运动,运动时间为t s,连接BE.当∠OBE= 30°时,t的值为______.

答案：
1或4 解析:如图,连接AB.当点E在点O的下方时,
∵ ∠OBE = 30°,∠OBC = 30°,
∴ 点E与点H重合.
∵ OB = 2cm,BC⊥AD,
∴ 易得OE = 1cm.
∴ DE = OD - OE = 1cm.
∴ t = 1.当点E'在点O的上方时,
∵ BC⊥AD,∠OBC = 30°,
∴ ∠BOH = 90° - ∠OBC = 60°.
∵ OB = OA,
∴ ∠OBA = 1/2∠BOH = 30°.
∵ ∠OBE' = 30°,
∴ 点E'和点A重合.
∴ DE' = 4cm.
∴ t = 4.综上所述,当∠OBE = 30°时,t的值为1或4.
　　　　

8. 如图,在平面直角坐标系中,点A、B的坐标分别是(0,2)、(4,0),P是直线y= 2x+2上的一动点,当以点P为圆心、PO长为半径的圆与△AOB的一条边所在的直线相切时,点P的坐标为______.

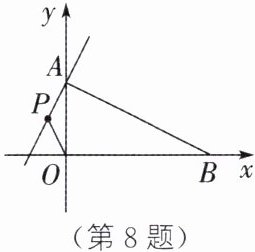
答案：
(-1/2,1)或(-1,0)或(0,2)
解析:记直线y = 2x + 2与x轴的交点为C,则易得点C的坐标为(-1,0).
∵ 点A、B的坐标分别是(0,2)、(4,0),
∴ 易得直线AB对应的函数表达式为y = -1/2x + 2,AC² = 5,AB² = 20,BC² = 25.
∴ AC² + AB² = BC².
∴ ∠CAB = 90°,即AC⊥AB.
∵ P是直线y = 2x + 2上的一动点,
∴ PA⊥AB.① 如图①,当⊙P与边AB所在的直线相切时,易知AC为⊙P的直径.
∴ PA = PC,即P为AC的中点.
∴ 点P的坐标为(-1/2,1).② 如图②,当⊙P与边AO所在的直线相切时,PO⊥AO,即点P在x轴上.
∴ 点P与点C重合.
∴ 点P的坐标为(-1,0).③ 如图③,当⊙P与边BO所在的直线相切时,PO⊥BO,即点P在y轴上.
∴ 点P与点A重合.
∴ 点P的坐标为(0,2).综上所述,点P的坐标为(-1/2,1)或(-1,0)或(0,2).
　　　
　　　
　　　

9. 在△ABC中,AB= 5,BC= 3,AC= 4,点P在∠ABC的平分线上,以点P为圆心作⊙P.
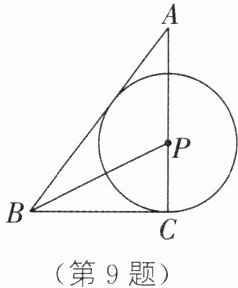
(1)如图,当⊙P经过点C时,求证：⊙P与直线AB相切.
(2)当⊙P同时与直线BC、AC相切时,⊙P的半径为______.

答案：

(1)如图①,过点P作PD⊥AB于点D.
∵ AB = 5,BC = 3,AC = 4,
∴ AB² = BC² + AC².
∴ ∠ACB = 90°.
∴ PC⊥BC.
∵ BP平分∠ABC,PC⊥BC,PD⊥AB,
∴ PC = PD.
∵ ⊙P经过点C,
∴ PC、PD为⊙P的半径.
又
∵ PD⊥AB,
∴ ⊙P与直线AB相切.
(2)1或3. 解析:如图②,当⊙P同时与直线BC、AC相切时,点P在∠ACB或∠ACM的平分线上.分两种情况讨论:① 当圆心在△ABC内部,即⊙P₁分别与BC、AC相切于点G、F时,连接P₁G、P₁F,过点P₁作P₁E⊥AB于点E.
∵ 点P₁在∠ABC的平分线上,P₁E⊥AB,P₁G⊥BC,
∴ P₁E = P₁G.设P₁G = P₁F = P₁E = r.连接AP₁、CP₁.
∵ P₁G⊥BC,P₁E⊥AB,P₁F⊥AC,
∴ S△ABC = S△ABP₁ + S△ACP₁ + S△BCP₁ = 1/2AB·P₁E + 1/2AC·P₁F + 1/2BC·P₁G = 1/2(AB + AC + BC)·r.
∴ r = 2S△ABC/(AB + AC + BC) = (2×1/2×3×4)/(5 + 4 + 3) = 1.② 当圆心在△ABC外部,即⊙P₂分别与直线BC、AC相切于点M、N时,连接P₂M、P₂N,过点P₂作P₂Q⊥BA,交BA的延长线于点Q.
∵ 点P₂在∠ABC的平分线上,P₂M⊥BC,P₂Q⊥AB,
∴ P₂M = P₂Q.设P₂M = P₂N = P₂Q = R.连接AP₂、CP₂.
∵ P₂M⊥BC,P₂Q⊥AB,P₂N⊥AC,
∴ S△ABC = S△ABP₂ + S△BCP₂ - S△ACP₂ = 1/2AB·P₂Q + 1/2BC·P₂M - 1/2AC·P₂N = 1/2(AB + BC - AC)·R.
∴ R = 2S△ABC/(AB + BC - AC) = (2×1/2×3×4)/(5 + 3 - 4) = 3.综上所述,⊙P的半径为1或3.