《2025年拔尖特训九年级数学上册苏科版》

12. 新考法·操作实践题 如图,数轴上点 $A$ 与点 $C$ 表示的数分别为1和3,$O$ 为原点,宸宸同学以 $C$ 为直角顶点作 $Rt\triangle ABC$,$BC = 1$,再以点 $A$ 为圆心,$AB$ 长为半径画圆,交数轴于 $D$、$E$ 两点。莲莲同学说：“若点 $D$、$E$ 分别表示数 $m$ 和 $n$,我发现 $x = m$ 是一元二次方程 $x^2 + bx - 4 = 0$ 的一个根。”琮琮说：“$x = n$ 一定不是此方程的根。”

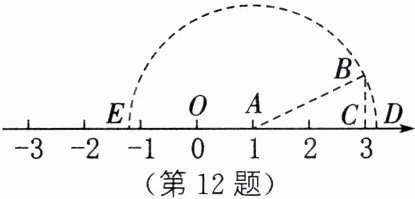
(1)请写出 $m$ 与 $n$ 的值。
(2)求出 $b$ 的值。
(3)你认为琮琮说得对吗？为什么？

答案：
(1)在Rt△ABC中,
∵BC=1,AC=2,
∴AB=$\sqrt{1^2+2^2}$=$\sqrt{5}$.
∴AE=AD=AB=$\sqrt{5}$.
∵点A表示的数为1,
∴OE=AE-OA=$\sqrt{5}$-1,OD=AD+OA=$\sqrt{5}$+1.
∴点D表示的数为$\sqrt{5}$+1,即m=$\sqrt{5}$+1;点E表示的数为-$\sqrt{5}$+1,即n=-$\sqrt{5}$+1.
(2)把x=$\sqrt{5}$+1代入方程x²+bx-4=0,得($\sqrt{5}$+1)²+($\sqrt{5}$+1)b-4=0,解得b=-2,即b的值为-2.
(3)琮琮说得不对.把x=-$\sqrt{5}$+1代入方程x²-2x-4=0.
∵左边=(-$\sqrt{5}$+1)²-2(-$\sqrt{5}$+1)-4=5-2$\sqrt{5}$+1+2$\sqrt{5}$-2-4=0,
∴左边=右边.
∴x=n是此方程的根.
∴琮琮说得不对.

13. 在关于 $x$ 的一元二次方程 $x^2 - 2ax + b = 0$ 中,若 $a^2 - b ＞ 0$,则称 $a$ 是该方程的“中点值”。
(1)方程 $x^2 - 8x + 3 = 0$ 的“中点值”是4。
(2)已知方程 $x^2 - mx + n = 0$ 的“中点值”是3,其中一个根是 $x = 2$,求 $mn$ 的值。
由题意,得$\frac{m}{2}$=3,解得m=6.把x=2,m=6代入x²-mx+n=0,得4-6×2+n=0,解得n=8.∴mn=6×8=48.

答案：
(1)4.
(2)由题意,得$\frac{m}{2}$=3,解得m=6.把x=2,m=6代入x²-mx+n=0,得4-6×2+n=0,解得n=8.
∴mn=6×8=48.

14. 已知下列三个关于 $x$ 的一元二次方程 $ax^2 + bx + c = 0$,$bx^2 + cx + a = 0$,$cx^2 + ax + b = 0$ 恰好有一个相同的实数根 $\alpha$,则 $a + b + c$ 的值为(A)
A.0
B.1
C.3
D.2

答案： A 解析:把x=a代入ax²+bx+c=0,bx²+cx+a=0,cx²+ax+b=0,得a·a²+ba+c=0,ba²+ca+a=0,ca²+a·a+b=0.相加,得(a+b+c)a²+(b+c+a)·a+(a+b+c)=0,即(a+b+c)(a²+a+1)=0.
∵a²+a+1=(a+$\frac{1}{2}$)²+$\frac{3}{4}$＞0,
∴a+b+c=0.

15. 阅读材料：
问题：已知方程 $x^2 + x - 1 = 0$,求一个一元二次方程,使它的根分别是已知方程的根的2倍。

解：设所求方程的根为 $y$,则 $y = 2x$。
$\therefore x = \frac{y}{2}$。
把 $x = \frac{y}{2}$ 代入已知方程 $x^2 + x - 1 = 0$,得 $\left(\frac{y}{2}\right)^2 + \frac{y}{2} - 1 = 0$。
化简,得 $y^2 + 2y - 4 = 0$。
这种利用方程根的替换求新方程的方法,我们称为“换根法”。
请用材料提供的“换根法”求新方程(把所求方程化成一般形式)。
(1)已知方程 $x^2 + x - 2 = 0$,求一个一元二次方程,使它的根分别是已知方程的根的相反数。
(2)已知关于 $x$ 的一元二次方程 $ax^2 + bx + c = 0(a \neq 0)$ 有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程的根的倒数。

答案：
(1)设所求方程的根为m,则m=-x.
∴x=-m.把x=-m代入已知方程x²+x-2=0,得(-m)²+(-m)-2=0.化简,得m²-m-2=0.
(2)设所求方程的根为n,则n=$\frac{1}{x}$.
∴x=$\frac{1}{n}$.把x=$\frac{1}{n}$代入已知方程ax²+bx+c=0(a≠0),得a($\frac{1}{n}$)²+b·$\frac{1}{n}$+c=0.去分母,得a+bn+cn²=0.若c=0,则原方程ax²+bx+c=0(a≠0)一定有一个根为0,不合题意.
∴c≠0.
∴所求方程为cn²+bn+a=0(c≠0).