《2025年拔尖特训九年级数学上册苏科版》

1. 如图,AB 是$\odot O$的直径,点 C、D 在$\odot O$上,且点 C、D 在 AB 的异侧,连接 AD、OD、OC.若$\angle AOC= 70^\circ$,且 AD$//$OC,则$\angle AOD$的度数为(D)

A.$70^\circ$
B.$60^\circ$
C.$50^\circ$
D.$40^\circ$

答案： D

2. 如图,点 A、D、G、M 在半圆 O 上,四边形 ABOC、DEOF、HMNO 均为矩形.设 BC = a,EF = b,NH = c,则下列各式中,正确的是(B)
A.$a ＞ b ＞ c$
B.$a = b = c$
C.$c ＞ a ＞ b$
D.$b ＞ c ＞ a$

答案： B

3. 如图,延长$\odot O$的弦 AB、半径 OC,两者交于点 D,BD = OA.若$\angle AOC= 120^\circ$,则$\angle D$的度数是______$20^{\circ}$.

答案： $20^{\circ}$

4. 如图,O 是$\angle EPF$的平分线上的一点,以点 O 为圆心的圆和$\angle EPF$的两边分别交于点 A、B 和点 C、D.AB 与 CD 相等吗？为什么？

答案： 相等
过点O作$OG\perp AB$于点G，$OH\perp CD$于点H，连接OA、OC、OB、OD.
∵O是$\angle EPF$平分线上的一点，
∴$OG = OH$.
在$Rt\triangle OBG$和$Rt\triangle ODH$中，
∵$OB = OD$，$OG = OH$，
∴$Rt\triangle OBG\cong Rt\triangle ODH$.
∴$BG = DH$，
同理，可得$AG = CH$.
∴$AG + BG = CH + DH$.
∴$AB = CD$.

5. 如图,AB 是$\odot O$的弦,OC$\perp$AB,垂足为 C,OD$//$AB,OC= $\frac{1}{2}$OD,则$\angle ABD$的度数为(D)
A.$90^\circ$
B.$95^\circ$
C.$100^\circ$
D.$105^\circ$

答案： D

6. 如图,将两个正方形按如图所示的方式放置(点 B、C、E 共线,点 D、C、G 共线),若 AB = 3,EF = 2,点 O 在线段 BC 上,以 OF 为半径作半圆 O,点 A、F 都在半圆 O 上,则 OD 的长是( B )
A.4
B.$\sqrt{10}$
C.$\sqrt{13}$
D.$\sqrt{26}$

答案： B　解析:如图，连接OA.
∵OF是半圆O的半径，
∴$OA = OF$.
∵四边形ABCD、四边形EFGC都是正方形，
∴$\angle ABC = \angle DCB = \angle FEC = 90^{\circ}$，$AB = BC = CD = 3$，$CE = EF = 2$.设$OC = x$，则$BO = BC - OC = 3 - x$，$OE = OC + CE = x + 2$.在$Rt\triangle ABO$和$Rt\triangle EFO$中，$AB^{2} + BO^{2} = OA^{2}$，$OE^{2} + EF^{2} = OF^{2}$，
∴$3^{2} + (3 - x)^{2} = OA^{2}$，$(x + 2)^{2} + 2^{2} = OF^{2}$.
∵$OA = OF$，
∴$3^{2} + (3 - x)^{2} = (x + 2)^{2} + 2^{2}$，解得$x = 1$，即$OC = 1$.在$Rt\triangle DOC$中，$DO^{2} = OC^{2} + DC^{2}$，
∴$OD = \sqrt{OC^{2} + CD^{2}} = \sqrt{1^{2} + 3^{2}} = \sqrt{10}$

7. 如图,P 是$\odot O$外一点,Q 是$\odot O$上的动点,线段 PQ 的中点为 M,连接 OP、OM.若$\odot O$的半径为 4,OP = 8,则 OM 长的最小值是2.

答案： 2

8. 如图,过 D、A、C 三点的圆的圆心为点 E,过 B、E、F 三点的圆的圆心为点 D.如果$\angle BAC= 66^\circ$,那么$\angle ABC= $16°.

答案： 16

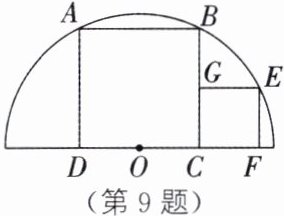
9. 如图,四边形 ABCD、四边形 EFCG 均为正方形,两个正方形彼此相邻且在半圆 O 内.若正方形 EFCG 的面积为$16\ cm^2$,则半圆 O 的半径为______$4\sqrt{5}$cm. 答案讲解

答案： $4\sqrt{5}$cm