《2025年一遍过八年级数学上册沪科版》

1 下列4组图形中,左边图形与右边图形成轴对称的是 ( )

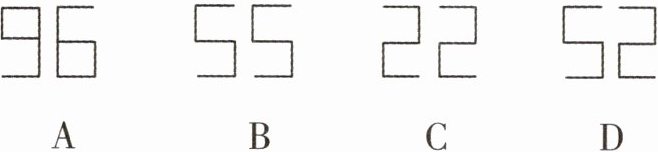
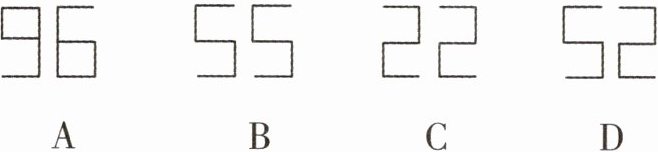
答案： D

2 [2024淮南谢家集区期中]小明照镜子时,发现衣服上的英文单词在镜子中呈现为“smtns”,则这个英文单词是____。

答案： maths

3 教材P124T3变式 如图,先画出△ABC关于直线$l_1$对称的$△A_1B_1C_1($直线$l_1$过点C),再画出$△A_1B_1C_1$关于直线$l_2$对称的$△A_2B_2C_2。$

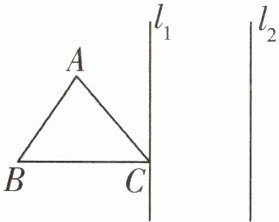
答案：
解:找出点A,B,C关于直线$l_{1}$的对称点$A_{1},B_{1},C_{1}$,然后顺次连接即可;再找出点$A_{1},B_{1},C_{1}$关于直线$l_{2}$的对称点$A_{2},B_{2},C_{2}$,然后顺次连接即可.$\triangle A_{1}B_{1}C_{1},\triangle A_{2}B_{2}C_{2}$如图所示.

名师点睛
此类题目考查利用轴对称变换作图,根据轴对称的性质,准确找出对应点的位置是解题的关键.

4 给出下列说法：①P是线段AB上的一点,直线l经过点P且l⊥AB,则l是线段AB的垂直平分线；②直线l经过线段AB的中点,则l是线段AB的垂直平分线；③经过线段AB的中点P且垂直于AB的直线l是线段AB的垂直平分线。其中正确的是____。(填序号)

答案： ③ ①当点P不是AB的中点时,l不平分线段AB,故①错误;②当直线l不垂直于AB时,l不是线段AB的垂直平分线,故②错误;③符合线段垂直平分线的定义,故③正确.

5 [2024河北中考]如图,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A,B的对称点分别是点C,D。下列不一定正确的是 ( )

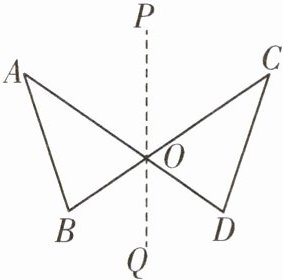
A.AD⊥BC

B.AC⊥PQ
C.△ABO≌△CDO
D.AC//BD

答案：
A 如图,连接AC,BD,$\because \triangle ABO$和$\triangle CDO$关于直线PQ对称,$\therefore \triangle ABO\cong \triangle CDO$,$PQ\perp AC$,$PQ\perp BD$,$\therefore AC// BD$,故选项B,C,D正确,不符合题意;AD不一定垂直BC,故选项A不一定正确,符合题意.

6 [2025六安裕安区期末]如图,将一张长方形纸片斜折过去,使顶点A落在A'处,BC为折痕,然后再把BE折过去,使之与BA'重合,折痕为BD,若∠ABC= 59°,则∠E'BD的度数为 ( )


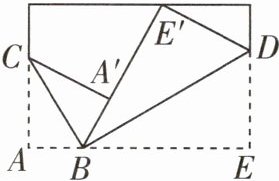
A.31°
B.32°
C.59°
D.62°

答案： A 根据折叠的性质,得$\angle ABC=\angle A'BC$,$\angle EBD=\angle E'BD$,$\because \angle ABC+\angle A'BC+\angle EBD+\angle E'BD=180^{\circ}$,$\therefore \angle ABC+\angle E'BD=90^{\circ}$,$\therefore \angle E'BD=90^{\circ}-59^{\circ}=31^{\circ}$.
归纳总结
解决折叠问题的关键是知道折痕所在的直线就是折叠前后的两个图形(折叠部分)的对称轴,所以它们的对应边、对应角分别相等.

7 [2025湖州期中]如图,AD所在直线是△ABC的对称轴,点E,F是AD上的两点。若BD= 2,AD= 3,则图中阴影部分的面积是____。

答案： 3 解题思路:
轴对称图形的性质$S_{\triangle BEF}=S_{\triangle CEF}$
$\because$AD所在直线是$\triangle ABC$的对称轴,$\therefore \triangle ABD$与$\triangle ACD$关于直线AD对称,$\therefore S_{\triangle ABD}=S_{\triangle ACD}$,$AD\perp BC$. $\because$点E,F是AD上的两点,$\therefore \triangle BEF$与$\triangle CEF$关于直线AD对称,$\therefore S_{\triangle EFB}=S_{\triangle EFC}$,$\therefore S_{阴影部分}=S_{\triangle ABE}+S_{\triangle EFC}+S_{\triangle BFD}=S_{\triangle ABD}=\frac{1}{2}BD\cdot AD=\frac{1}{2}× 2× 3=3$.

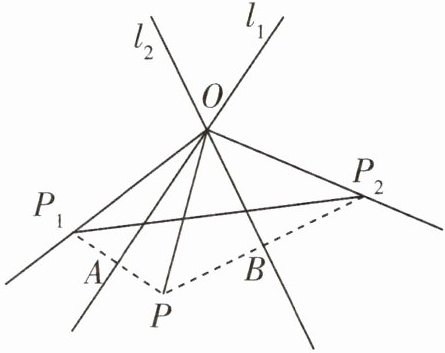
8 如图,直线$l_1,l_2$交于点O,点P关于$l_1,l_2$的对称点分别为$P_1,P_2。$
(1)若∠AOB= 60°,则$∠P_1OP_2= ____；$
(2)若$OP= 3,P_1P_2= 5,$求$△P_1OP_2$的周长。

答案：
(1)$120^{\circ}$
因为点P关于$l_{1},l_{2}$的对称点分别为$P_{1},P_{2}$,所以$\angle P_{1}OA=\angle AOP$,$\angle P_{2}OB=\angle POB$,所以$\angle P_{1}OP_{2}=2(\angle AOP+\angle POB)=2\angle AOB=2× 60^{\circ}=120^{\circ}$.
(2)因为点P关于$l_{1},l_{2}$的对称点分别为$P_{1},P_{2}$,所以$OP_{1}=OP=OP_{2}=3$.因为$P_{1}P_{2}=5$,所以$\triangle P_{1}OP_{2}$的周长为$OP_{1}+OP_{2}+P_{1}P_{2}=3+3+5=11$.