《2025年一遍过八年级数学上册沪科版》

答案 P48
【问题情境】
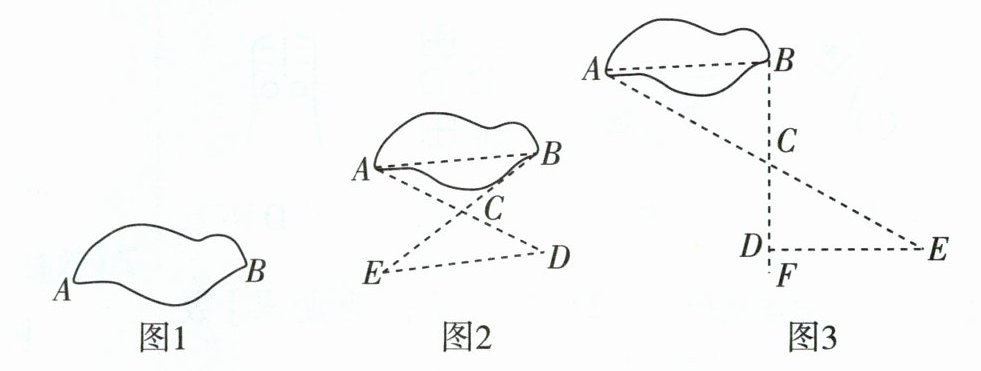
学校为开展数学实践活动,成立了以小明为首的户外测量小组,测量小组带有测量工具:绳子、拉尺、小红旗、测角器(可测量两个点分别到测量者连线之间的夹角大小).该测量小组的任务是测量某池塘不能直接到达的两个端点A,B之间的距离(如图1).
【方案设计】
同学们想出了如下的两种方案:
方案①:如图2,先在平地上取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,BC至点E,使DC= AC,EC= BC,最后量出DE的长度就是AB的长度.
方案②:如图3,过点B作AB的垂线BF,在BF上取C,D两点,使BC= CD,接着过点D作BD的垂线DE,在垂线上选一点E,使A,C,E三点在一条直线上,则测出DE的长即是AB的长.
【问题解决】
(1)方案①是否可行?请说明理由.
(2)方案②是否可行?请说明理由.
(3)假设池塘南面(即点D,E附近区域)没有足够空地(或空地有障碍物或不可直达等不可测量情况),而点B的右侧区域有足够空地并可用于测量,请你设计一个可行的测量方案(在图1中画出图形),并说明理由.

答案：

(1)方案①可行.理由如下:
在△ABC和△DEC中,{AC=DC,∠ACB=∠DCE,CB=CE,
∴△ABC≌△DEC(SAS),
∴DE=AB.
(2)方案②可行.理由如下:
∵AB⊥BD,ED⊥BD,
∴∠ABC=∠EDC=90°.
在△ABC和△EDC中,{∠ACB=∠ECD,CB=CD,∠ABC=∠EDC,
∴△ABC≌△EDC(ASA),
∴DE=AB.
(3)答案不唯一,合理即可.
方案:如图,过点B作BD⊥AB,再由点D观测,在AB的延长线上取一点C,使∠BDC=∠BDA.这时只要测出BC的长即为A,B之间的距离.

理由如下:
∵BD⊥AB,
∴∠ABD=∠CBD=90°.
在△ABD和△CBD中,{∠ABD=∠CBD,BD=BD,∠BDA=∠BDC,
∴△ABD≌△CBD(ASA),
∴AB=BC.