第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
5 [2025合肥庐阳区期末]为进一步推动绿色生态文明建设,走可持续发展之路,某工厂在生产过程中同步进行污水处理,有两种处理方案.
方案1:污水纳入污水处理厂统一处理,每生产1件产品需付7元的排污费;
方案2:积极响应“无废城市”号召,使用专业设备,通过有效方法,对污水进行循环利用.每生产1件产品需付1元的设备原料费,并且设备损耗费为每月b元.
若工厂每月生产x件产品,产品的成本价(不含污水处理费)为25元/件,出厂价为50元/件,方案1、方案2的月利润y(元)与x(件)之间的函数关系如图所示.结合图象回答问题:
(1)填空:$a= $____,$b= $____.
(2)当工厂每月生产300件产品时,两种方案的月利润相差多少元?
(3)当两种方案的月利润相差1500元时,求x的值.

方案1:污水纳入污水处理厂统一处理,每生产1件产品需付7元的排污费;
方案2:积极响应“无废城市”号召,使用专业设备,通过有效方法,对污水进行循环利用.每生产1件产品需付1元的设备原料费,并且设备损耗费为每月b元.
若工厂每月生产x件产品,产品的成本价(不含污水处理费)为25元/件,出厂价为50元/件,方案1、方案2的月利润y(元)与x(件)之间的函数关系如图所示.结合图象回答问题:
(1)填空:$a= $____,$b= $____.
(2)当工厂每月生产300件产品时,两种方案的月利润相差多少元?
(3)当两种方案的月利润相差1500元时,求x的值.

答案:
解:
(1)500 3000 根据题意,方案 1 的月利润$y_{1}$(元)与 x(件)之间的函数表达式为$y_{1}=(50-25-7)x=18x$,方案 2 的月利润$y_{2}$(元)与 x(件)之间的函数表达式为$y_{2}=(50-25-1)x-b=24x-b$。将$(a,9000)$分别代入$y_{1}=18x$和$y_{2}=24x-b$,得$\left\{\begin{array}{l} 18a=9000,\\ 24a-b=9000,\end{array}\right.$解得$\left\{\begin{array}{l} a=500,\\ b=3000.\end{array}\right.$
(2)由
(1)可知,$y_{1}=18x$,$y_{2}=24x-3000$。当$x=300$时,$y_{1}=18×300=5400$,$y_{2}=24×300-3000=4200$,$5400-4200=1200$(元)。答:两种方案的月利润相差 1200 元。
(3)根据题意,得$|y_{2}-y_{1}|=1500$,即$|24x-3000-18x|=1500$。解得$x=250$或 750。答:x 的值为 250 或 750。
(1)500 3000 根据题意,方案 1 的月利润$y_{1}$(元)与 x(件)之间的函数表达式为$y_{1}=(50-25-7)x=18x$,方案 2 的月利润$y_{2}$(元)与 x(件)之间的函数表达式为$y_{2}=(50-25-1)x-b=24x-b$。将$(a,9000)$分别代入$y_{1}=18x$和$y_{2}=24x-b$,得$\left\{\begin{array}{l} 18a=9000,\\ 24a-b=9000,\end{array}\right.$解得$\left\{\begin{array}{l} a=500,\\ b=3000.\end{array}\right.$
(2)由
(1)可知,$y_{1}=18x$,$y_{2}=24x-3000$。当$x=300$时,$y_{1}=18×300=5400$,$y_{2}=24×300-3000=4200$,$5400-4200=1200$(元)。答:两种方案的月利润相差 1200 元。
(3)根据题意,得$|y_{2}-y_{1}|=1500$,即$|24x-3000-18x|=1500$。解得$x=250$或 750。答:x 的值为 250 或 750。
6 [2025合肥瑶海区期中]某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/辆和8吨/辆,运往甲、乙两地的运费如下表:
|车型|运费|
| |运往甲地/(元/辆)|运往乙地/(元/辆)|
|大货车|720|800|
|小货车|500|650|
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,运往甲、乙两地的总运费为w元,求w关于a的函数表达式;
(3)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.
|车型|运费|
| |运往甲地/(元/辆)|运往乙地/(元/辆)|
|大货车|720|800|
|小货车|500|650|
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,运往甲、乙两地的总运费为w元,求w关于a的函数表达式;
(3)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.
答案:
解题思路:
(1)根据大、小两种货车共 18 辆,以及两种车所运的货物的和是 192 吨,列方程或方程组即可求解;
(2)先用含 a 的式子表示出每种车对应路线的费用,再将它们相加即得总运费 w 关于 a 的函数表达式;
(3)根据运往甲地的物资不少于 96 吨,即可列出不等式求得 a 的范围,再根据 a 是整数,即可确定 a 的值,根据
(2)中的函数表达式,即可确定 w 的最小值及运输方案。
解:
(1)设大货车用 x 辆,则小货车用$(18-x)$辆。根据题意,得$14x+8(18-x)=192$,解得$x=8$,则$18-x=18-8=10$。答:大货车用 8 辆,小货车用 10 辆。
(2)因为前往甲地的大货车是 a 辆,所以前往乙地的大货车是$(8-a)$辆,前往甲地的小货车是$(10-a)$辆,前往乙地的小货车是$[10-(10-a)]$辆。根据题意,得$w=720a+800(8-a)+500(10-a)+650[10-(10-a)]=70a+11400(0≤a≤8且a为整数)$。
(3)根据题意,得$14a+8(10-a)≥96$。解得$a≥\frac {8}{3}$。又因为$0≤a≤8$,所以$\frac {8}{3}≤a≤8$且 a 为整数,即 a 的取值可以是 3,4,5,6,7,8。对于$w=70a+11400$,因为$70>0$,所以 w 随 a 的增大而增大,所以当$a=3$时,w 最小,最小值为$70×3+11400=11610$。答:使总运费最低的货车调配方案是 3 辆大货车,7 辆小货车前往甲地;5 辆大货车,3 辆小货车前往乙地。最低总运费为 11610 元。
(1)根据大、小两种货车共 18 辆,以及两种车所运的货物的和是 192 吨,列方程或方程组即可求解;
(2)先用含 a 的式子表示出每种车对应路线的费用,再将它们相加即得总运费 w 关于 a 的函数表达式;
(3)根据运往甲地的物资不少于 96 吨,即可列出不等式求得 a 的范围,再根据 a 是整数,即可确定 a 的值,根据
(2)中的函数表达式,即可确定 w 的最小值及运输方案。
解:
(1)设大货车用 x 辆,则小货车用$(18-x)$辆。根据题意,得$14x+8(18-x)=192$,解得$x=8$,则$18-x=18-8=10$。答:大货车用 8 辆,小货车用 10 辆。
(2)因为前往甲地的大货车是 a 辆,所以前往乙地的大货车是$(8-a)$辆,前往甲地的小货车是$(10-a)$辆,前往乙地的小货车是$[10-(10-a)]$辆。根据题意,得$w=720a+800(8-a)+500(10-a)+650[10-(10-a)]=70a+11400(0≤a≤8且a为整数)$。
(3)根据题意,得$14a+8(10-a)≥96$。解得$a≥\frac {8}{3}$。又因为$0≤a≤8$,所以$\frac {8}{3}≤a≤8$且 a 为整数,即 a 的取值可以是 3,4,5,6,7,8。对于$w=70a+11400$,因为$70>0$,所以 w 随 a 的增大而增大,所以当$a=3$时,w 最小,最小值为$70×3+11400=11610$。答:使总运费最低的货车调配方案是 3 辆大货车,7 辆小货车前往甲地;5 辆大货车,3 辆小货车前往乙地。最低总运费为 11610 元。
7 [2025六安期中]综合与实践.
【问题背景】某市2025年初中学业体育水平考试的总分值拟提高到80分,考试项目增加5项,其中技能类考试项目除篮球和足球外增加了排球垫球.某校为更好地开展排球课程,计划购买一批排球,该市两家体育用品商店分别推出了自己的优惠方案.
甲商店:若购买超过20个,超过部分每个按排球标价的八折出售.
乙商店:若购买超过15个,超过部分每个按排球标价的九五折再优惠10元出售.
【问题研究】
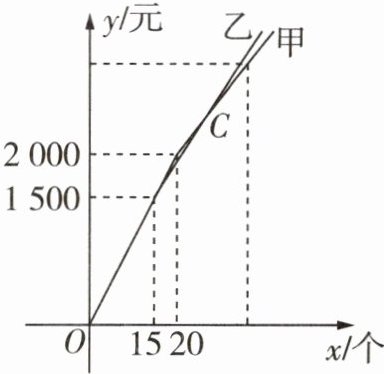
若用x表示购买排球的数量,y表示购买排球的总价,其函数图象如图所示.
【问题解决】
(1)每个排球的标价是多少元?
(2)当$x>20$时,甲商店应付的总价$y_{甲}$与数量x之间的函数表达式为____;
当$x>15$时,乙商店应付的总价$y_{乙}$与数量x之间的函数表达式为____.
(3)求点C的坐标,并根据图象直接写出选择哪家商店购买排球更合算.
【问题背景】某市2025年初中学业体育水平考试的总分值拟提高到80分,考试项目增加5项,其中技能类考试项目除篮球和足球外增加了排球垫球.某校为更好地开展排球课程,计划购买一批排球,该市两家体育用品商店分别推出了自己的优惠方案.
甲商店:若购买超过20个,超过部分每个按排球标价的八折出售.
乙商店:若购买超过15个,超过部分每个按排球标价的九五折再优惠10元出售.
【问题研究】
若用x表示购买排球的数量,y表示购买排球的总价,其函数图象如图所示.
【问题解决】
(1)每个排球的标价是多少元?
(2)当$x>20$时,甲商店应付的总价$y_{甲}$与数量x之间的函数表达式为____;
当$x>15$时,乙商店应付的总价$y_{乙}$与数量x之间的函数表达式为____.
(3)求点C的坐标,并根据图象直接写出选择哪家商店购买排球更合算.

答案:
解:
(1)由题中图象,可知甲商店标价为$2000÷20 = 100$(元/个),乙商店标价为$1500÷15 = 100$(元/个),两个商店排球的标价是一样的,所以每个排球的标价是 100 元。
(2)$y_{甲}=80x + 400$,$y_{乙}=85x + 225$。当$x>20$时,$y_{甲}=100×20 + 0.8×(x - 20)=80x + 400$,所以$y_{甲}$与数量 x 之间的函数表达式为$y_{甲}=80x + 400$;当$x>15$时,$y_{乙}=100×15+(100×0.95 - 10)(x - 15)=85x + 225$,所以$y_{乙}$与数量 x 之间的函数表达式为$y_{乙}=85x + 225$。
(3)因为点 C 是两个函数图象的交点,所以$\begin{cases}80x + 400 = y \\ 85x + 225 = y \end{cases}$,解得$\begin{cases}x = 35 \\ y = 3200 \end{cases}$,所以点 C 的坐标为$(35,3200)$。由图象可知,当$0≤x≤15$或$x = 35$时,在甲、乙两家商店所付的钱数相同;当$15<x<35$时,选择乙商店更合算;当$x>35$时,选择甲商店更合算。
(1)由题中图象,可知甲商店标价为$2000÷20 = 100$(元/个),乙商店标价为$1500÷15 = 100$(元/个),两个商店排球的标价是一样的,所以每个排球的标价是 100 元。
(2)$y_{甲}=80x + 400$,$y_{乙}=85x + 225$。当$x>20$时,$y_{甲}=100×20 + 0.8×(x - 20)=80x + 400$,所以$y_{甲}$与数量 x 之间的函数表达式为$y_{甲}=80x + 400$;当$x>15$时,$y_{乙}=100×15+(100×0.95 - 10)(x - 15)=85x + 225$,所以$y_{乙}$与数量 x 之间的函数表达式为$y_{乙}=85x + 225$。
(3)因为点 C 是两个函数图象的交点,所以$\begin{cases}80x + 400 = y \\ 85x + 225 = y \end{cases}$,解得$\begin{cases}x = 35 \\ y = 3200 \end{cases}$,所以点 C 的坐标为$(35,3200)$。由图象可知,当$0≤x≤15$或$x = 35$时,在甲、乙两家商店所付的钱数相同;当$15<x<35$时,选择乙商店更合算;当$x>35$时,选择甲商店更合算。
查看更多完整答案,请扫码查看


