《2025年一遍过八年级数学上册沪科版》

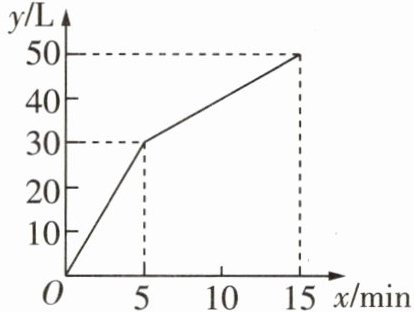
1 [2024 哈尔滨中考]一个有进水管与出水管的容器,从某时刻开始 5 min 内只进水不出水,在随后的 10 min 内既进水又出水,每分钟的进水量和出水量是两个常数. 容器内的水量 y(单位:L)与时间 x(单位:min)之间的关系如图所示,当 x = 9 min 时,y = ( )


A.36 L
B.38 L
C.40 L
D.42 L

答案： B 设当5≤x≤15时,直线对应的函数表达式为y=kx+b(k≠0).因为直线经过点(5,30),(15,50),所以{5k+b=30,15k+b=50,所以{k=2,b=20,所以直线对应的函数表达式为y=2x+20(5≤x≤15).令x=9,y=2×9+20=38.

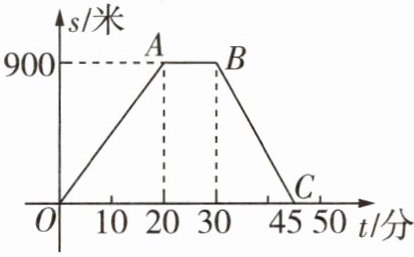
2 新趋势·结论开放[2024 攀枝花中考]如图,折线 OABC 表示了距离 s(米)与时间 t(分)之间的函数关系.
(1)分别直接写出线段 OA,AB 所对应的函数表达式,并注明相应的 t 的取值范围;
(2)请你想象一个符合函数图象的实际情境,并用语言进行描述(不必描述具体的速度).

答案： 解:
(1)线段OA对应的函数表达式为s=45t(0≤t≤20),线段AB对应的函数表达式为s=900(20≤t≤30).
(2)小明从家步行去图书馆,图书馆距离小明家900米,用时20分钟,然后小明在图书馆看书用了10分钟,再步行回家,用时15分钟.(答案不唯一,符合图象即可)

3 [2024 合肥包河区期中]某水果超市欲购买某种水果进行销售. 若一次性购买不超过 40 千克,则每千克该种水果的价格为 30 元;若一次性购买超过 40 千克,则超过的部分,每千克水果打八折. 设水果超市购买该种水果 x 千克,付款 y 元.
(1)求 y 关于 x 的函数表达式.
(2)若一次性购买该种水果 100 千克,需要付款多少元?

答案： 解:
(1)由题意,得y={30x(0≤x≤40),40×30+30×0.8×(x-40)(x＞40),即y={30x(0≤x≤40),24x+240(x＞40).
(2)当x=100时,y=24×100+240=2640.答:需要付款2640元.

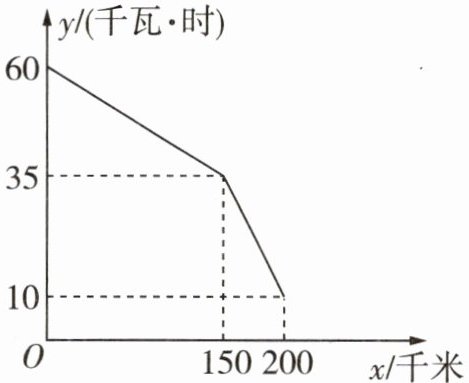
4 [2024 合肥蜀山区期中]如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量 y(千瓦·时)关于已行驶路程 x(千米)的函数图象.
(1)根据图象,直接写出蓄电池剩余电量为 35 千瓦·时时汽车已行驶的路程为______千米;当 0 ≤ x ≤ 150 时,1 千瓦·时的电量汽车能行驶的路程为______千米.
(2)当 150 ≤ x ≤ 200 时,求 y 关于 x 的函数表达式,并计算当汽车已行驶 180 千米时,蓄电池的剩余电量.

答案： 解:
(1)150 6
(2)设y=kx+b(k≠0).
把点(150,35),(200,10)的坐标分别代入,得{150k+b=35,200k+b=10,解得{k=-0.5,b=110,所以y关于x的函数表达式为y=-0.5x+110.
当x=180时,y=-0.5×180+110=20,故当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦·时.