第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
过全章 题串练透全章知识 答案 P22
已知一次函数$y_{1}= (m - 1)x + 3 - m$,$y_{2}= (1 + 2n)x + n + 3$。
【基础设问】
(1)若一次函数$y_{1}$是正比例函数,则$m = $____。
(2)若点$(1,a)$,$(-4,b)是一次函数y_{1}$图象上的两个点,且$a < b$,则$m$的取值范围是____。
(3)若一次函数$y_{1}$的图象不经过第二象限,则$m$的取值范围为____。
(4)一次函数$y_{1}$的图象恒过点____。
(5)若一次函数$y_{1}的图象经过点(-3,-1)$,且与直线$y = tx + 5$平行,则$t$的值为____。
【能力设问】
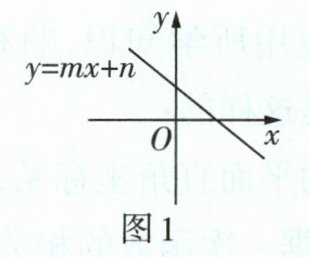
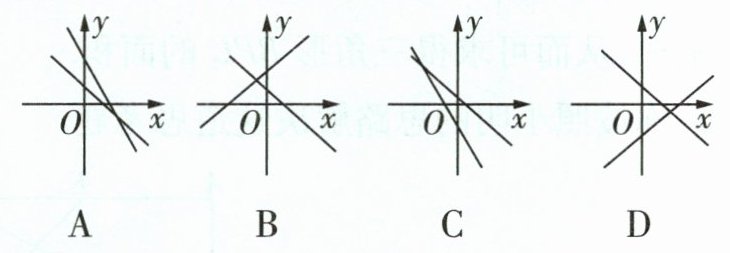
(6)若函数$y = mx + n$的图象如图1所示,函数$y_{1}和y_{2}$在同一平面直角坐标系中的图象可能是( )
(7)当$n = 1$时,
①一次函数$y_{2}$的表达式为____,当$-1\leqslant x\leqslant 2$时,函数$y_{2}$的最大值为____。
②将一次函数$y_{2}$的图象向上平移2个单位长度,再向下平移3个单位长度,得到的函数图象的表达式为____。
③一次函数$y_{2}$的图象与坐标轴的交点坐标为____,它与坐标轴围成的三角形的面积为____。
【拓展设问】
(8)如图2,函数$y_{1}的图象与y轴交于点A$,函数$y_{2}的图象与y轴交于点B$,两函数图象交于点$P(3,-1)$。
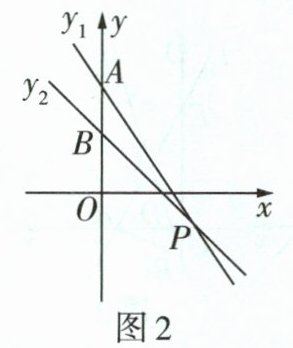
①关于$x$,$y的方程组\begin{cases}(m - 1)x + 3 = m + y,\\(1 + 2n)x + 3 = y - n\end{cases} $的解为____。
②求关于$x的不等式(m - 1)x - m > (1 + 2n)x + n$的解集。
③若点$M$,$N分别是直线x = c(0 < c < 3)与函数y_{1}$,$y_{2}$的图象的交点,且$MN = \frac{1}{3}AB$,求$c$的值。
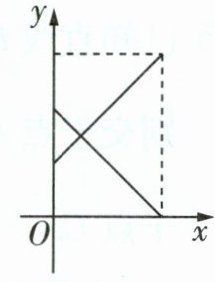
(9)新趋势·结论开放 令$m = 2$,$n = -1$,则一次函数$y_{1}与y_{2}$的部分图象如图所示,请你给这个图象配上一个合适的情境。
已知一次函数$y_{1}= (m - 1)x + 3 - m$,$y_{2}= (1 + 2n)x + n + 3$。
【基础设问】
(1)若一次函数$y_{1}$是正比例函数,则$m = $____。
(2)若点$(1,a)$,$(-4,b)是一次函数y_{1}$图象上的两个点,且$a < b$,则$m$的取值范围是____。
(3)若一次函数$y_{1}$的图象不经过第二象限,则$m$的取值范围为____。
(4)一次函数$y_{1}$的图象恒过点____。
(5)若一次函数$y_{1}的图象经过点(-3,-1)$,且与直线$y = tx + 5$平行,则$t$的值为____。
【能力设问】
(6)若函数$y = mx + n$的图象如图1所示,函数$y_{1}和y_{2}$在同一平面直角坐标系中的图象可能是( )


(7)当$n = 1$时,
①一次函数$y_{2}$的表达式为____,当$-1\leqslant x\leqslant 2$时,函数$y_{2}$的最大值为____。
②将一次函数$y_{2}$的图象向上平移2个单位长度,再向下平移3个单位长度,得到的函数图象的表达式为____。
③一次函数$y_{2}$的图象与坐标轴的交点坐标为____,它与坐标轴围成的三角形的面积为____。
【拓展设问】
(8)如图2,函数$y_{1}的图象与y轴交于点A$,函数$y_{2}的图象与y轴交于点B$,两函数图象交于点$P(3,-1)$。

①关于$x$,$y的方程组\begin{cases}(m - 1)x + 3 = m + y,\\(1 + 2n)x + 3 = y - n\end{cases} $的解为____。
②求关于$x的不等式(m - 1)x - m > (1 + 2n)x + n$的解集。
③若点$M$,$N分别是直线x = c(0 < c < 3)与函数y_{1}$,$y_{2}$的图象的交点,且$MN = \frac{1}{3}AB$,求$c$的值。
(9)新趋势·结论开放 令$m = 2$,$n = -1$,则一次函数$y_{1}与y_{2}$的部分图象如图所示,请你给这个图象配上一个合适的情境。

答案:
(1)3
(2)m<1 由题意,得y₁随x的增大而减小,所以m - 1<0,所以m<1.
(3)m≥3 由题意,得一次函数y₁的图象经过第一、三、四象限或第一、三象限,所以m - 1>0,3 - m≤0,解得m≥3.
(4)(1,2) 对于y₁=(m - 1)x + 3 - m,整理得m(x - 1)=y₁ + x - 3,易知m是不等于1的任意常数,所以x - 1=0,y₁ + x - 3=0,解得x = 1,y₁ = 2,所以一次函数y₁的图象恒过点(1,2).
(5)$\frac{3}{4}$ 因为一次函数y₁的图象经过点(-3,-1),所以(m - 1)×(-3)+3 - m=-1,解得$m=\frac{7}{4}$.因为一次函数y₁的图象与直线y = tx + 5平行,所以$t=m - 1=\frac{7}{4}-1=\frac{3}{4}$.
(6)B 由题图1可知,m<0,n>0,则m - 1<0,3 - m>0,1 + 2n>0,n + 3>0,所以一次函数y₁的图象经过第一、二、四象限,一次函数y₂的图象经过第一、二、三象限,结合选项知B符合题意.
(7)①y₂=3x + 4 10 当n = 1时,一次函数y₂=3x + 4.因为3>0,所以y₂随x的增大而增大,当x = 2时,y₂取得最大值,为10.
②y = 3x + 3 经过题中所述的平移后,得到的函数图象的表达式为y = 3x + 4+2 - 3,即y = 3x + 3.
③$(-\frac{4}{3},0)$,$(0,4)$ $\frac{8}{3}$ 令y₂ = 0,得$x=-\frac{4}{3}$,令x = 0,得y₂ = 4,故函数y₂的图象与坐标轴的交点坐标为$(-\frac{4}{3},0)$,$(0,4)$,所以函数y₂的图象与坐标轴围成的三角形的面积为$\frac{1}{2}×4×\frac{4}{3}=\frac{8}{3}$.
(8)①$\left\{\begin{array}{l} x = 3\\ y = -1\end{array}\right. $
②(m - 1)x - m>(1 + 2n)x + n可化为(m - 1)x + 3 - m>(1 + 2n)x + 3 + n.结合题图2,可知当x<3时,函数y₁的图象在函数y₂的图象的上方,所以关于x的不等式(m - 1)x - m>(1 + 2n)x + n的解集为x<3.
③由题意可知,将(3,-1)代入y₁的表达式中,得3(m - 1)+3 - m=-1,解得$m=-\frac{1}{2}$,所以$y_{1}=-\frac{3}{2}x+\frac{7}{2}$.同理,可得n=-1,所以y₂=-x + 2.令x = 0,得$y_{A}=\frac{7}{2}$,$y_{B}=2$,所以$AB=\frac{7}{2}-2=\frac{3}{2}$.令x = c(0<c<3),得$y_{M}=\frac{7}{2}-\frac{3}{2}c$,$y_{N}=2 - c$.由题图2可知,当0<x<3时,y₁>y₂,所以$y_{M}>y_{N}$,所以$MN=(\frac{7}{2}-\frac{3}{2}c)-(2 - c)=\frac{3}{2}-\frac{1}{2}c$.因为$MN=\frac{1}{3}AB$,所以$\frac{3}{2}-\frac{1}{2}c=\frac{1}{3}×\frac{3}{2}=\frac{1}{2}$,解得c = 2,即c的值为2.
(9)答案略.(答案不唯一,合理即可)
(1)3
(2)m<1 由题意,得y₁随x的增大而减小,所以m - 1<0,所以m<1.
(3)m≥3 由题意,得一次函数y₁的图象经过第一、三、四象限或第一、三象限,所以m - 1>0,3 - m≤0,解得m≥3.
(4)(1,2) 对于y₁=(m - 1)x + 3 - m,整理得m(x - 1)=y₁ + x - 3,易知m是不等于1的任意常数,所以x - 1=0,y₁ + x - 3=0,解得x = 1,y₁ = 2,所以一次函数y₁的图象恒过点(1,2).
(5)$\frac{3}{4}$ 因为一次函数y₁的图象经过点(-3,-1),所以(m - 1)×(-3)+3 - m=-1,解得$m=\frac{7}{4}$.因为一次函数y₁的图象与直线y = tx + 5平行,所以$t=m - 1=\frac{7}{4}-1=\frac{3}{4}$.
(6)B 由题图1可知,m<0,n>0,则m - 1<0,3 - m>0,1 + 2n>0,n + 3>0,所以一次函数y₁的图象经过第一、二、四象限,一次函数y₂的图象经过第一、二、三象限,结合选项知B符合题意.
(7)①y₂=3x + 4 10 当n = 1时,一次函数y₂=3x + 4.因为3>0,所以y₂随x的增大而增大,当x = 2时,y₂取得最大值,为10.
②y = 3x + 3 经过题中所述的平移后,得到的函数图象的表达式为y = 3x + 4+2 - 3,即y = 3x + 3.
③$(-\frac{4}{3},0)$,$(0,4)$ $\frac{8}{3}$ 令y₂ = 0,得$x=-\frac{4}{3}$,令x = 0,得y₂ = 4,故函数y₂的图象与坐标轴的交点坐标为$(-\frac{4}{3},0)$,$(0,4)$,所以函数y₂的图象与坐标轴围成的三角形的面积为$\frac{1}{2}×4×\frac{4}{3}=\frac{8}{3}$.
(8)①$\left\{\begin{array}{l} x = 3\\ y = -1\end{array}\right. $
②(m - 1)x - m>(1 + 2n)x + n可化为(m - 1)x + 3 - m>(1 + 2n)x + 3 + n.结合题图2,可知当x<3时,函数y₁的图象在函数y₂的图象的上方,所以关于x的不等式(m - 1)x - m>(1 + 2n)x + n的解集为x<3.
③由题意可知,将(3,-1)代入y₁的表达式中,得3(m - 1)+3 - m=-1,解得$m=-\frac{1}{2}$,所以$y_{1}=-\frac{3}{2}x+\frac{7}{2}$.同理,可得n=-1,所以y₂=-x + 2.令x = 0,得$y_{A}=\frac{7}{2}$,$y_{B}=2$,所以$AB=\frac{7}{2}-2=\frac{3}{2}$.令x = c(0<c<3),得$y_{M}=\frac{7}{2}-\frac{3}{2}c$,$y_{N}=2 - c$.由题图2可知,当0<x<3时,y₁>y₂,所以$y_{M}>y_{N}$,所以$MN=(\frac{7}{2}-\frac{3}{2}c)-(2 - c)=\frac{3}{2}-\frac{1}{2}c$.因为$MN=\frac{1}{3}AB$,所以$\frac{3}{2}-\frac{1}{2}c=\frac{1}{3}×\frac{3}{2}=\frac{1}{2}$,解得c = 2,即c的值为2.
(9)答案略.(答案不唯一,合理即可)
查看更多完整答案,请扫码查看


