《2025年一遍过八年级数学上册沪科版》

10 已知正比例函数 $ y = - 3 m x $,若 $ y $随 $ x $的增大而增大,则点 $ P ( m , 5 ) $在 ( )

A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： B 因为$y$随$x$的增大而增大，所以$-3m ＞ 0$，所以$m ＜ 0$，所以点$P(m，5)$在第二象限..

11 [2024 武汉华中师大附中二测]如果一个正比例函数的图象经过不同象限的两点 $ A ( 2 , m ) , B ( n , 3 ) $,那么一定有 ( )

A.$ m ＞ 0 , n ＞ 0 $
B.$ m ＞ 0 , n ＜ 0 $
C.$ m ＜ 0 , n ＞ 0 $
D.$ m ＜ 0 , n ＜ 0 $

答案： D 当$m ＞ 0，n ＞ 0$时，$A，B$两点在第一象限，故选项A错误；当$m ＞ 0，n ＜ 0$或$m ＜ 0，n ＞ 0$时，$A，B$两点不在同一个正比例函数图象上，故选项B，C错误；当$m ＜ 0，n ＜ 0$时，$A，B$两点分别在第四、二象限，两点有可能在同一个正比例函数图象上，故选项D正确.

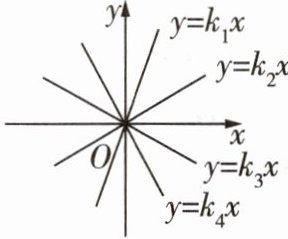
12 [教材 P37T3 变式][2024 兰州三十五中 期 中]已知 4 个正比例函数 $ y = k _ { 1 } x , y = k _ { 2 } x , y = k _ { 3 } x , y = k _ { 4 } x $的图象如图所示,则下列结论成立的是 ( )

A.$ k _ { 1 } ＞ k _ { 2 } ＞ k _ { 3 } ＞ k _ { 4 } $

B.$ k _ { 1 } ＞ k _ { 2 } ＞ k _ { 4 } ＞ k _ { 3 } $
C.$ k _ { 2 } ＞ k _ { 1 } ＞ k _ { 3 } ＞ k _ { 4 } $
D.$ k _ { 4 } ＞ k _ { 3 } ＞ k _ { 2 } ＞ k _ { 1 } $

答案： A 通解 根据直线经过的象限，知$k_3 ＜ 0，k_4 ＜ 0，k_1 ＞ 0，k_2 ＞ 0$，再根据直线越“陡”，$|k|$越大，知$|k_1| ＞ |k_2|，|k_4| ＞ |k_3|$，故$k_1 ＞ k_2 ＞ k_3 ＞ k_4$. 另解 过点$(1，0)$作$x$轴的垂线，与函数$y = k_1x，y = k_2x，y = k_3x，y = k_4x$的图象分别交于点$(1，k_1)，(1，k_2)，(1，k_3)，(1，k_4)$，由交点的位置可得$k_1 ＞ k_2 ＞ k_3 ＞ k_4$.

13 [一题多解][2024 郑州中原区期末]对于正比例函数 $ y = k x ( k \neq 0 ) $,当自变量 $ x $的值减小 2 时,函数 $ y $的值增加 6,则 $ k $的值为____.

答案： -3 通解 根据题意，得$y + 6 = k(x - 2)$，即$y + 6 = kx - 2k$，而$y = kx$，所以$-2k = 6$，解得$k = -3$. 另解 因为正比例函数$y = kx$的图象是一条经过原点的直线，且当自变量$x$的值减小2时，函数$y$的值增加6，所以直线$y = kx$经过第二、四象限，且当$x = -2$时，$y = 6$，如图，则$6 = -2k$，解得$k = -3$.

14 [易错题][2025 合肥蜀山区期中]已知正比例函数 $ y = k x $,当 $ - 4 \leq x \leq 4 $时,函数有最大值 3,求 $ k $的值.

答案： 解：当$k ＞ 0$时，函数值$y$随$x$的增大而增大，所以当$x = 4$时，$y = 4k = 3$，解得$k = \frac{3}{4}$. 当$k ＜ 0$时，函数值$y$随$x$的增大而减小，所以当$x = -4$时，$y = -4k = 3$，解得$k = -\frac{3}{4}$. 综上所述，$k$的值为$\frac{3}{4}$或$-\frac{3}{4}$.

15 [推理能力]如图,过原点的两条直线分别为 $ l _ { 1 } : y = 2 x , l _ { 2 } : y = - x $. 过点 $ A ( 1 , 0 ) $作 $ x $轴的垂线,与 $ l _ { 1 } $交于点 $ A _ { 1 } $,过点 $ A _ { 1 } $作 $ y $轴的垂线,与 $ l _ { 2 } $交于点 $ A _ { 2 } $,过点 $ A _ { 2 } $作 $ x $轴的垂线,与 $ l _ { 1 } $交于点 $ A _ { 3 } $,过点 $ A _ { 3 } $作 $ y $轴的垂线,与 $ l _ { 2 } $交于点 $ A _ { 4 } $,过点 $ A _ { 4 } $作 $ x $轴的垂线,与 $ l _ { 1 } $交于点 $ A _ { 5 } … … $依次进行下去,则点 $ A _ { 20 } $的坐标为____.

答案： $(1024,-1024)$ 对于$y = 2x$，当$x = 1$时，$y = 2$，所以点$A_1$的坐标为$(1，2)$；对于$y = -x$，当$y = 2$时，$x = -2$，所以点$A_2$的坐标为$(-2，2)$；同理，可得$A_3(-2，-4)，A_4(4，-4)，A_5(4，8)，A_6(-8，8)，A_7(-8，-16)，A_8(16，-16)，A_9(16，32)，\cdots$，所以$A_{4n + 1}(2^{2n}，2^{2n + 1})，A_{4n + 2}(-2^{2n + 1}，2^{2n + 1})，A_{4n + 3}(-2^{2n + 2}，-2^{2n + 2})，A_{4n + 4}(2^{2n + 2}(-2^{2n + 2})（n$为自然数），所以点$A_{20}$的坐标为$(2^{2 × 4 + 2}，-2^{2 × 4 + 2})$，即$(1024，-1024)$.

16 [推理能力]如图,已知四边形 $ A B C D $是正方形,点 $ B , C $分别在正比例函数 $ y = 2 x $和 $ y = k x $的图象上,点 $ A , D $是 $ x $轴上的两点.
(1)若此正方形的边长为 2,则 $ k = $____.
(2)若此正方形的边长为 $ a $,则 $ k $的值是否会发生变化? 若不会发生变化,请说明理由;若会发生变化,试求出 $ k $的值.

答案： 解：
(1)$\frac{2}{3}$ 因为正方形的边长为2，所以$AB = CD = AD = 2$. 在$y = 2x$中，令$y = 2$，得$x = 1$所以$OA = 1$，所以$OD = 1 + 2 = 3$，所以点$C$的坐标为$(3，2)$. 将点$C$的坐标$(3，2)$代入$y = kx$，得$2 = 3k$，解得$k = \frac{2}{3}$.
(2)$k$的值不会发生变化. 理由如下： 因为正方形的边长为$a$，所以$AB = CD = AD = a$. 在$y = 2x$中，令$y = a$，得$x = \frac{a}{2}$，所以$OA = \frac{a}{2}$，所以$OD = \frac{3}{2}a$，所以点$C$的坐标为$(\frac{3}{2}a，a)$. 将点$C$的坐标$(\frac{3}{2}a，a)$代入$y = kx$，得$a = k \cdot \frac{3}{2}a$，解得$k = \frac{2}{3}$，所以$k$的值不会发生变化.