第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
8 [2025六安金安区段考]若将平面直角坐标系中的点$P(a - 2,2a + 1)向左平移1$个单位长度后得到的点位于第二象限,则$a$的取值范围为( )
A.$0 < a < 2$
B.$-\frac{1}{2} < a < 1$
C.$-\frac{1}{2} < a < 2$
D.$-\frac{1}{2} < a < 3$
A.$0 < a < 2$
B.$-\frac{1}{2} < a < 1$
C.$-\frac{1}{2} < a < 2$
D.$-\frac{1}{2} < a < 3$
答案:
D 将点P(a - 2,2a + 1)向左平移1个单位长度后得到的点的坐标为(a - 3,2a + 1),因为该点位于第二象限,所以{a - 3<0,2a + 1>0,解得-1/2 < a < 3.
9 [2024威海中考]定义新运算:①在平面直角坐标系中,$\{a,b\}$表示动点从原点出发,沿着$x轴正方向(a\geq0)或负方向(a < 0)平移\vert a\vert$个单位长度,再沿着$y轴正方向(b\geq0)或负方向(b < 0)平移\vert b\vert$个单位长度。例如,动点从原点出发,沿着$x轴负方向平移2$个单位长度,再沿着$y轴正方向平移1$个单位长度,记作$\{-2,1\}$。②加法运算法则:$\{a,b\} + \{c,d\} = \{a + c,b + d\}$,其中$a$,$b$,$c$,$d$为实数。若$\{3,5\} + \{m,n\} = \{-1,2\}$,则下列结论正确的是( )
A.$m = 2$,$n = 7$
B.$m = -4$,$n = -3$
C.$m = 4$,$n = 3$
D.$m = -4$,$n = 3$
A.$m = 2$,$n = 7$
B.$m = -4$,$n = -3$
C.$m = 4$,$n = 3$
D.$m = -4$,$n = 3$
答案:
B 由题知,3 + m = -1,5 + n = 2,解得m = -4,n = -3.
10 [2025池州段考]如图,将三角形$AOB沿x轴向右平移得到三角形CDE$,点$B的坐标为(3,0)$,$DB = 1$,则点$E$的坐标为( )
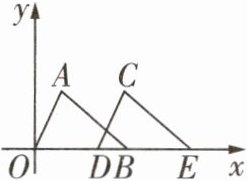
A.$(4,0)$
B.$(5,0)$
C.$(6,0)$
D.$(7,0)$

A.$(4,0)$
B.$(5,0)$
C.$(6,0)$
D.$(7,0)$
答案:
B 因为点B的坐标为(3,0),所以OB = 3.所以OD = OB - DB = 3 - 1 = 2.所以D(2,0).所以三角形AOB向右平移了2个单位长度得到三角形CDE(点拨:由对应点的坐标,得出图形的平移规律).因为点B的坐标为(3,0),所以点E的坐标为(3 + 2,0),即(5,0).
11 [2024济南外国语学校月考]如图是一组密码的一部分,为了保密,许多情况下会采用不同的“密钥”,请你运用所学知识找到破译的“密钥”。目前已破译出“守初心”的对应口令是“担使命”。根据你发现的“密钥”,破译出“找差距”的对应口令是______。


答案:
抓落实 因为"守初心"的对应口令是"担使命","守"所对应的字为"担",是从"守"字开始先向左平移1个单位长度,再向上平移2个单位长度后得到的,其他各个字的对应字也是这样得到的,所以"找差距"的对应口令是"抓落实".
12 [2024合肥瑶海区期中]如图所示,在平面直角坐标系中,已知点$A(-3,3)$,$B(-5,1)$,$C(-2,0)$,$P(a,b)是三角形ABC的边AC$上任意一点,三角形$ABC经过平移后得到三角形A_1B_1C_1$,点$P的对应点为P_1(a + 6,b - 2)$。
(1)点$C_1$的坐标为______。
(2)在图中画出三角形$A_1B_1C_1$。
(3)三角形$AOA_1$的面积为______。
(4)在$x轴上找一点Q$,使三角形$B_1CQ的面积等于三角形COC_1$面积的一半,直接写出点$Q$的坐标。
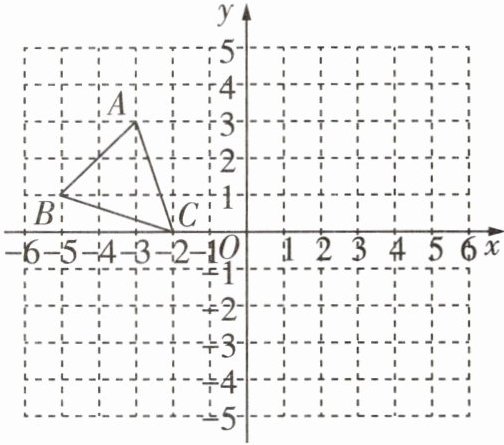
(1)点$C_1$的坐标为______。
(2)在图中画出三角形$A_1B_1C_1$。
(3)三角形$AOA_1$的面积为______。
(4)在$x轴上找一点Q$,使三角形$B_1CQ的面积等于三角形COC_1$面积的一半,直接写出点$Q$的坐标。

答案:
(1)(4,-2)
(2)三角形A₁B₁C₁如图所示.
(3)6三角形AOA₁的面积为1/2×(1 + 3)×6 - 1/2×1×3 - 1/2×3×3 = 6.
(4)点Q的坐标为(0,0)或(-4,0).
(1)(4,-2)
(2)三角形A₁B₁C₁如图所示.

(3)6三角形AOA₁的面积为1/2×(1 + 3)×6 - 1/2×1×3 - 1/2×3×3 = 6.
(4)点Q的坐标为(0,0)或(-4,0).
13 [推理能力][2024河北中考]在平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于$0$的点称为“和点”。将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以$3$所得的余数(当余数为$0$时,向右平移;当余数为$1$时,向上平移;当余数为$2$时,向左平移),每次平移$1$个单位长度。
例:“和点”$P(2,1)按上述规则连续平移3$次后,到达点$P_3(2,2)$,其平移过程如下:$P(2,1)\xrightarrow[\text{余0}]{\text{右}}P_1(3,1)\xrightarrow[\text{余1}]{\text{上}}P_2(3,2)\xrightarrow[\text{余2}]{\text{左}}P_3(2,2)$。
若“和点”$Q按上述规则连续平移16$次后,到达点$Q_{16}(-1,9)$,则点$Q$的坐标为( )
A.$(6,1)或(7,1)$
B.$(15,-7)或(8,0)$
C.$(6,0)或(8,0)$
D.$(5,1)或(7,1)$
例:“和点”$P(2,1)按上述规则连续平移3$次后,到达点$P_3(2,2)$,其平移过程如下:$P(2,1)\xrightarrow[\text{余0}]{\text{右}}P_1(3,1)\xrightarrow[\text{余1}]{\text{上}}P_2(3,2)\xrightarrow[\text{余2}]{\text{左}}P_3(2,2)$。
若“和点”$Q按上述规则连续平移16$次后,到达点$Q_{16}(-1,9)$,则点$Q$的坐标为( )
A.$(6,1)或(7,1)$
B.$(15,-7)或(8,0)$
C.$(6,0)或(8,0)$
D.$(5,1)或(7,1)$
答案:
D 当点Q的余数("余数"指横、纵坐标之和除以3所得的余数)分别为0,1,2时,平移规律如下:由上可知,当点Q的余数为0时,连续平移16次后的余数为2;当点Q的余数为1时,连续平移16次后的余数为1;当点Q的余数为2时,连续平移16次后的余数为2.设Q(m,n).因为Q₁₆的余数为2,所以分两种情况讨论.①当点Q的余数为0时,点Q向右平移1个单位长度后,得到点Q₁(m + 1,n),结合平移规律知Q₁₆的坐标为(m + 1 - 7,n + 8),即(m - 6,n + 8),所以m - 6 = -1,n + 8 = 9,解得m = 5,n = 1.所以Q(5,1).②当点Q的余数为2时,Q₁₆的坐标为(m - 8,n + 8),所以m - 8 = -1,n + 8 = 9,解得m = 7,n = 1.所以Q(7,1).故选D.
D 当点Q的余数("余数"指横、纵坐标之和除以3所得的余数)分别为0,1,2时,平移规律如下:由上可知,当点Q的余数为0时,连续平移16次后的余数为2;当点Q的余数为1时,连续平移16次后的余数为1;当点Q的余数为2时,连续平移16次后的余数为2.设Q(m,n).因为Q₁₆的余数为2,所以分两种情况讨论.①当点Q的余数为0时,点Q向右平移1个单位长度后,得到点Q₁(m + 1,n),结合平移规律知Q₁₆的坐标为(m + 1 - 7,n + 8),即(m - 6,n + 8),所以m - 6 = -1,n + 8 = 9,解得m = 5,n = 1.所以Q(5,1).②当点Q的余数为2时,Q₁₆的坐标为(m - 8,n + 8),所以m - 8 = -1,n + 8 = 9,解得m = 7,n = 1.所以Q(7,1).故选D.

查看更多完整答案,请扫码查看


