《2025年一遍过八年级数学上册沪科版》

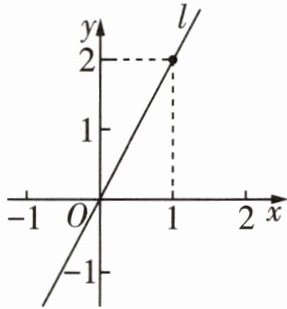
1 [2025成都段考]如图,直线l所对应的函数表达式为 ( )

A.$y= -2x$

B.$y= 2x$
C.$y= -\frac{1}{2}x$
D.$y= \frac{1}{2}x$

答案： B 设直线l的表达式为y=kx(直线l经过原点,符合正比例函数图象的特征).将(1,2)代入,得k=2,直线l所对应的函数表达式为y=2x.

2 一次函数$y= kx+b(k≠0)的图象过点(-2,1)和点(0,4)$,那么k,b的值分别为 ( )

A.$-\frac{2}{3},4$
B.$\frac{2}{3},4$
C.$-\frac{3}{2},4$
D.$\frac{3}{2},4$

答案： D 因为一次函数y=kx+b(k≠0)的图象过点(-2,1)和点(0,4),所以{ -2k+b=1,b=4,解得{ k=3/2,b=4.

3 教材P42T3变式[2025合肥期末]某一次函数的图象与直线$y= \frac{1}{2}x+6$平行,并且经过点$(-2,-4)$,则该一次函数的表达式为 ( )

A.$y= -\frac{1}{2}x-5$
B.$y= \frac{1}{2}x+3$
C.$y= \frac{1}{2}x-3$
D.$y= -2x-8$

答案： C 设该一次函数的表达式为y=kx+b.因为这个一次函数的图象与直线y=1/2x+6平行,所以k=1/2.把(-2,-4)代入y=1/2x+b,得b=-3,所以该一次函数的表达式为y=1/2x-3.

4 [2025合肥蜀山区期中]根据下表中一次函数的自变量x与函数y的对应值,可得p的值为____.
|x|-2|0|1|
|y|3|p|0|

答案： 1 设一次函数的表达式为y=kx+b(k≠0).因为当x=-2时,y=3;当x=1时,y=0,所以{ -2k+b=3,k+b=0,解得{ k=-1,b=1,所以一次函数的表达式为y=-x+1.当x=0时,y=1,即p=1.

5 教材P48T13变式[2025阜阳段考]已知y与$x+1$成正比例,当$x= 2$时,$y= 6$.
(1)求y与x之间的函数表达式;
(2)试判断点$(4,4)$是否在该函数的图象上,并说明理由.

答案： 解:
(1)因为y与x+1成正比例,所以设y与x+1的函数表达式为y=k(x+1).把(2,6)代入,得(2+1)k=6,解得k=2,所以y与x的函数表达式为y=2(x+1)=2x+2.
(2)点(4,4)不在函数y=2x+2的图象上.理由如下:令x=4,则y=2×4+2=10≠4,所以点(4,4)不在该函数的图象上.

6 [2025铜陵铜官区段考]已知点A,B,C的坐标分别为$A(-1,5),B(-\frac{3}{2},6),C(2,-1)$,试判断A,B,C三点是否在同一直线上,并说明理由.

答案： 解:A,B,C三点在同一直线上.理由如下:设直线AC的函数表达式为y=kx+b(k≠0).把A(-1,5),C(2,-1)代入,得{ -k+b=5,2k+b=-1,解得{ k=-2,b=3,所以直线AC的函数表达式为y=-2x+3.把x=-3/2代入y=-2x+3,得y=-2×(-3/2)+3=6,所以点B(-3/2,6)在直线AC上,所以A,B,C三点在同一直线上.

7 [2025合肥蜀山区段考]如图,直线AB与x轴交于点$A(1,0)$,与y轴交于点$B(0,-2)$.
(1)求直线AB的函数表达式.
(2)直线AB上是否存在点C,使三角形BOC的面积为2?若存在,求出点C的坐标;若不存在,请说明理由.

答案： 解:
(1)设直线AB的函数表达式为y=kx+b(k≠0).由题意可得{ k+b=0,b=-2,解得{ k=2,b=-2,所以直线AB的函数表达式为y=2x-2.
(2)直线AB上存在点C使三角形BOC的面积为2.因为点B(0,-2),所以OB=2.设点C的坐标为(x,y).因为S三角形BOC=1/2×OB×|x|=2,即1/2×2×|x|=2,解得x=±2.当x=2时,y=2×2-2=2;当x=-2时,y=2×(-2)-2=-6.所以点C的坐标是(2,2)或(-2,-6).