《2025年一遍过八年级数学上册沪科版》

10 [2024 蚌埠蚌山区段考]如图,在△ABC 中,∠C = 90°,D,E 是 AC 上两点,且 AE = DE,BD 平分∠EBC,那么下列说法中不一定正确的是( )

A.BE 是△ABD 的中线
B.BD 是△BCE 的角平分线
C.∠1 = ∠2 = ∠3
D.BC 是△BDE 的高线

答案： C

11 新趋势·数学文化 [2023 安徽中考]清初数学家梅文鼎在著作《平三角举要》中,对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明,证明过程中创造性地设计直角三角形,得出了一个结论：如图,AD 是锐角三角形 ABC 的高,则 BD = $\frac{1}{2}(BC + \frac{AB^{2} - AC^{2}}{BC})$。当 AB = 7,BC = 6,AC = 5 时,CD = ______。

答案： 1

12 易错题 [2025 合肥庐阳区段考]已知 AD 是△ABC 的高,若∠BAD = 65°,∠CAD = 30°,则∠BAC 的度数为______。

答案： 95°或 35°

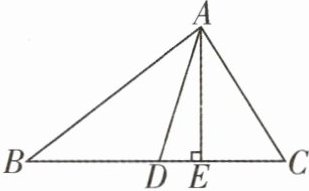
13 如图,在△ABC 中,AE 为边 BC 上的高,点 D 为边 BC 上的一点,连接 AD。
(1)当 AD 为边 BC 上的中线时,若 AE = 4,△ABC 的面积为 24,求 CD 的长。
(2)当 AD 为∠BAC 的平分线时。
①若∠B = 35°,∠C = 65°,求∠DAE 的度数；
②若∠C - ∠B = 20°,则∠DAE = ______°。

答案： 解:
(1)因为AE为边BC上的高,AE=4,△ABC的面积为24,所以 $\frac{1}{2}BC\cdot AE=24$,所以BC=12.因为AD为边BC上的中线,所以 $CD=\frac{1}{2}BC=6$.
(2)①因为∠B=35°,∠C=65°,所以∠BAC=180°-∠B-∠C=180°-35°-65°=80°.因为AD平分∠BAC,所以∠BAD=$\frac{1}{2}$∠BAC=40°.因为AE⊥BC,所以∠AEB=90°,所以∠BAE=180°-∠AEB-∠B=180°-90°-35°=55°,所以∠DAE=∠BAE-∠BAD=55°-40°=15°.②10

14 推理能力 已知△ABC 的两条高分别是 4 和 12,若第三条高也为整数,则第三条高可能为( )

A.3 或 4
B.1 或 2
C.2 或 3
D.4 或 5

答案： D

1 已知两中线 [2024 六安期末]如图,BD 是△ABC 的中线,点 E 是 BD 的中点,连接 CE。若△ABC 的面积为 12,则△BCE 的面积为( )

A.6
B.4
C.3
D.不能确定

答案： C

2 已知两中线 [2025 合肥庐阳区期中]如图,在△ABC 中,点 D 是 BC 上一点,BE 是△ABD 的中线,若△ABC 的面积是 24,则△BCE 的面积是( )

A.15
B.12
C.7.5
D.6

答案： B

3 已知四中线 [2024 亳州期末]如图,在△ABC 中,D,E,F 分别为 BC,AD,CE 的中点,且 $S_{△ABC} = 16 cm^{2}$,则阴影部分△BEF 的面积为( )


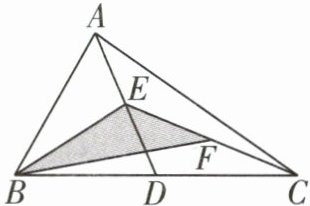
A.$2 cm^{2}$
B.$4 cm^{2}$
C.$6 cm^{2}$
D.$8 cm^{2}$

答案： B