《2025年一遍过八年级数学上册沪科版》

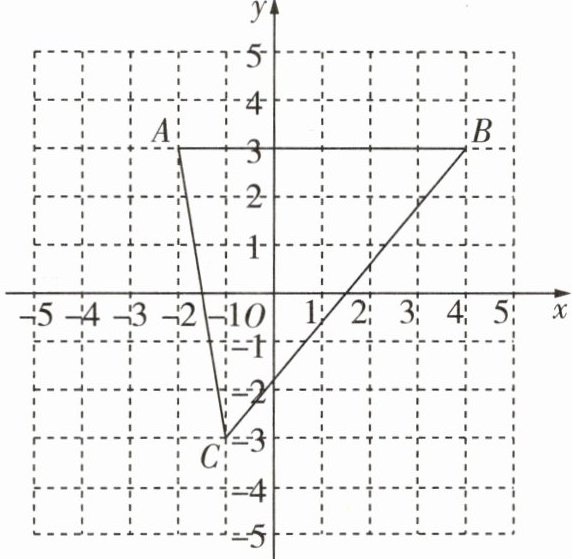
1 如图,已知$A(-2,3),B(4,3),C(-1,-3)$,则三角形 ABC 的面积为____.

答案： 18 因为A(-2,3),B(4,3),C(-1,-3),所以AB=4-(-2)=6,点C到边AB的距离为3-(-3)=6(点拨:点A,B的纵坐标相同,故AB//x轴),所以三角形ABC的面积为$\frac{1}{2}×6×6=18$.

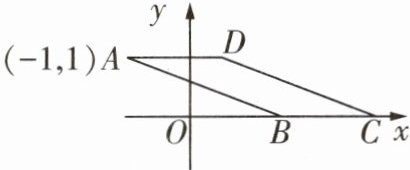
2 [2025济南莱芜区期末]如图,平行四边形 ABCD 的顶点 A 的坐标为$(-1,1)$,点 B,C 在x轴上.若平行四边形 ABCD 的面积为$\frac {3}{2}$,则点 D 的坐标为____.

答案： ($\frac{1}{2}$,1) 因为平行四边形ABCD的面积为$\frac{3}{2}$,点A的坐标为(-1,1),所以AD×1=$\frac{3}{2}$,所以AD=$\frac{3}{2}$,所以D(-1+$\frac{3}{2}$,1),即($\frac{1}{2}$,1).

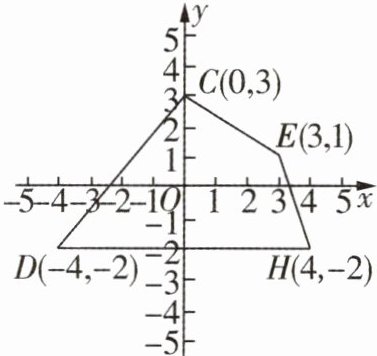
3 一题多解 四边形 CDHE 在平面直角坐标系中的位置如图所示,求四边形 CDHE 的面积.

答案：
解:通解 如图1,设DH交y轴于点G,过点E作EF⊥DH于点F,则$S_{四边形CDHE}=S_{三角形CDG}+S_{梯形CGFE}+S_{三角形EFH}=\frac{1}{2}×4×5+\frac{1}{2}×(3+5)×3+\frac{1}{2}×1×3=23.5$.
　　　　　　　　
另解 如图2,分别过点D,H作y轴的平行线,与过点C的x轴的平行线相交于点A,B,过点E作EM//x轴,交BH于点M,则$S_{四边形CDHE}=S_{长方形ABHD}-S_{三角形ACD}-S_{三角形EMH}-S_{梯形EMBC}=8×5-\frac{1}{2}×4×5-\frac{1}{2}×1×3-\frac{1}{2}×(1+4)×2=23.5$.
　　　　　　　　

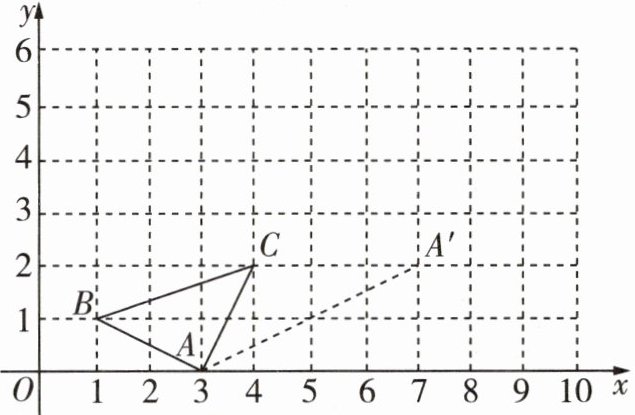
4 [2024淄博期末]在平面直角坐标系中,三角形 ABC 的三个顶点的位置如图所示,现将三角形 ABC 平移,使得点 A 移至图中点$A'$的位置.
(1)平移后所得三角形$A'B'C'的顶点B'$的坐标为____,$C'$的坐标为____(点$B',C'$分别为点 B,C 的对应点);
(2)求平移过程中 AB 扫过的面积.

答案：

(1)(5,3) (8,4)如图,三角形A'B'C'为平移后的三角形,则B'(5,3),C'(8,4).
(2)如图,平移过程中AB扫过的面积为$S_{四边形ABB'A'}=S_{长方形DEFG}-S_{三角形ABD}-S_{三角形AEA'}-S_{三角形A'FB'}-S_{三角形BCB'}=6×3-\frac{1}{2}×1×2-\frac{1}{2}×2×4-\frac{1}{2}×1×2-\frac{1}{2}×2×4=8$.