《2025年一遍过八年级数学上册沪科版》

1 如图,点B,C分别在∠EAF的边AE,AF上,点D在线段AC上。下列是△ABD的外角的是( )


A.∠BCF
B.∠CBE
C.∠DBC
D.∠BDF

答案： D

2 新情境 [2025十堰期末]体育课上的侧压腿动作(如图1)可以抽象为几何图形(如图2),如果∠1= 120°,那么∠2的度数是( )

A.30°
B.40°
C.60°
D.120°

答案： 根据三角形外角的性质得，∠1=∠2+90°，所以∠2=∠1-90°=120°-90°=30°.

3 一题多解 [2024巴中中考]如图,直线m//n,一块含有30°的直角三角板按如图所示放置。若∠1= 40°,则∠2的大小为( )

A.70°
B.60°
C.50°
D.40°

答案：
通解 如图1，因为m//n，所以∠3=∠2. 因为∠1=∠4=40°(对顶角相等)，所以∠3=30°+∠4=30°+40°=70°，所以∠2=70°.
另解 如图2，过点A作直线p//n，所以∠1=∠3=40°. 因为m//n，n//p，所以m//p，所以∠2=∠BAC=30°+∠3=30°+40°=70°.

4 [2025淮北杜集区期中]如图,点D在△ABC的边BC上,∠B：∠BAD= 2：3,∠ADC= 80°,则∠B的度数为______。

答案： 32° 设∠B=2x，则∠BAD=3x(方程思想). 因为∠ADC=∠B+∠BAD，所以2x+3x=80°，解得x=16°，所以∠B=2×16°=32°.

5 [2025芜湖期中]如图,在△ABC中,沿图中虚线剪去∠C,若∠1+∠2= 260°,则∠C的度数为______。

答案：
80° 如图，
∵∠1=∠C+∠DEC，∠2=∠C+∠EDC，
∴∠1+∠2=∠C+∠DEC+∠EDC+∠C.
∵∠C+∠DEC+∠EDC=180°，
∴∠1+∠2=∠C+180°，
∴∠C=260°-180°=80°.

归纳总结
“A”字型
如图，∠1+∠2=180°+∠A.

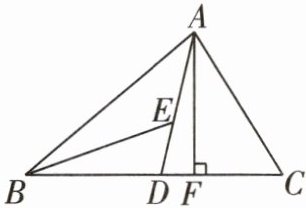
6 [2025上海青浦区段考]如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线,交AD于点E。若∠BED= 60°,∠BAD= 40°,求∠BAF的大小。

答案： 解：因为∠BED=∠ABE+∠BAD，所以∠ABE=∠BED-∠BAD=60°-40°=20°. 因为BE平分∠ABD，所以∠ABD=2∠ABE=40°. 因为AF为△ABC的高，所以∠AFB=90°，所以∠BAF=90°-∠ABF=90°-40°=50°.

7 一题多解 教材P87T7变式 如图,∠A= 37°,∠B= 28°,∠ADB= 148°,求∠C的度数。

答案：
解：通解 如图，连接CD并延长至点E.
∵∠ADE=∠A+∠ACD，
∴∠ACD=∠ADE-∠A=∠ADE-37°. 同理可得∠BCD=∠BDE-∠B=∠BDE-28°.
∵∠ACB=∠ACD+∠BCD，∠ADB=148°，
∴∠ACB=∠ADE-37°+∠BDE-28°=∠ADB-37°-28°=148°-37°-28°=83°.
另解一 如图，延长AD交BC于点F.
∵∠ADB=∠DFB+∠B，∠DFB=∠A+∠C，
∴∠ADB=∠A+∠C+∠B，
∴∠C=∠ADB-∠A-∠B=148°-37°-28°=83°.
另解二 如图，连接AB. 在△ADB中，∠1+∠2+∠ADB=180°，在△ABC中,∠1+∠2+∠CAD+∠CBD+∠C=180°，
∴∠C=∠ADB-∠CAD-∠CBD，即∠C=148°-37°-28°=83°.

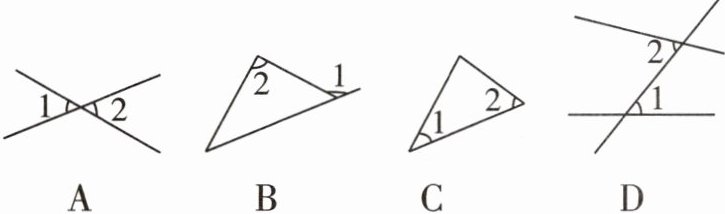
8 下列图形中能够说明∠1＞∠2的是( )

答案： B A中∠1=∠2，故本选项不符合题意；B中由三角形的外角大于与它不相邻的任何一个内角可知∠1＞∠2，故本选项符合题意；C中∠1和∠2的大小关系不能确定，故本选项不符合题意；D中延长直线会在右侧有交点得出∠2＞∠1，故本选项不符合题意.

9 如图,已知在△ABC中,∠1是它的一个外角,点E为边AC上一点,点D在边BC的延长线上,连接DE,则下列结论中不一定正确的是( )


A.∠1＞∠2
B.∠1＞∠3
C.∠3＞∠5
D.∠4＞∠5

答案： D 根据三角形外角的性质可知∠1＞∠3，∠3＞∠2，∠3＞∠5，所以∠1＞∠2，而∠4与∠5的大小无法判定.