《2025年一遍过八年级数学上册沪科版》

1 [2025 芜湖期末]如图,△ABC 的中线 AD,BE,CF 交于点 O。若△ABC 的面积是 14,则阴影部分的面积是( )


A.5
B.7
C.8.5
D.10.5

答案： B

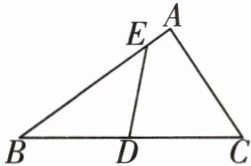
2 如图,在△ABC 中,AB = 10 cm,AC = 6 cm,D 是 BC 的中点,点 E 在边 AB 上。
(1)若△BDE 的周长与四边形 ACDE 的周长相等,求线段 AE 的长。
(2)若△ABC 的周长被 DE 分成的两部分的差是 2 cm,求线段 AE 的长。

答案： 解:
(1)因为△BDE的周长与四边形ACDE的周长相等,所以BE+BD+DE=AE+AC+DC+DE.因为点D是BC的中点,所以BD=DC,所以BE=AE+AC.因为AB=10cm,AC=6cm,所以10 - AE=AE+6,所以AE=2cm.
(2)由题意及
(1),得BE=AE+AC+2或BE=AE+AC - 2.又因为AB=BE+AE=10cm,AC=6cm,所以AE=1cm或3cm.

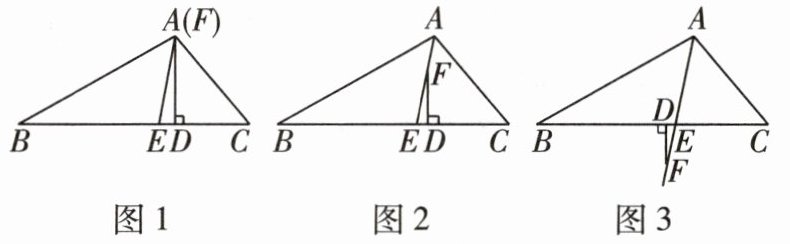
3 教材 P87T9 变式 [2024 安庆期中]在△ABC 中,∠C ＞ ∠B,AE 平分∠BAC,F 为射线 AE 上一点(不与点 E 重合),且 FD⊥BC 于点 D。
(1)如图 1,如果点 F 与点 A 重合,且∠C = 50°,∠B = 30°,求∠EFD 的度数。
(2)如图 2,如果点 F 在线段 AE 上(不与点 A 重合),此时∠EFD 与∠C - ∠B 有怎样的数量关系？并说明理由。
(3)如图 3,如果点 F 在△ABC 的外部,此时∠EFD 与∠C - ∠B 的数量关系是否会发生变化？请说明理由。

答案： 解:
(1)因为∠C=50°,∠B=30°,所以∠BAC=180°-50°-30°=100°.因为AE平分∠BAC,所以∠CAE=50°.因为FD⊥BC,所以∠FDC=90°,所以∠CFD=180°-90°-50°=40°,所以∠EFD=∠CAE-∠CFD=10°.
(2)$\angle EFD=\frac{1}{2}(\angle C-\angle B)$.理由如下:因为AE平分∠BAC,所以$\angle EAC=\frac{1}{2}\angle BAC=\frac{180^\circ-\angle C-\angle B}{2}=90^\circ-\frac{1}{2}(\angle C+\angle B)$.在△AEC中,$\angle AEC+\angle EAC+\angle C=180^\circ$,所以$\angle AEC=180^\circ-\angle C-\angle EAC=180^\circ-\angle C-90^\circ+\frac{1}{2}(\angle C+\angle B)=90^\circ+\frac{1}{2}(\angle B-\angle C)$.因为FD⊥BC,所以∠FDE=90°,所以$\angle EFD=180^\circ-\angle FDE-\angle AEC=180^\circ-90^\circ-90^\circ-\frac{1}{2}(\angle B-\angle C)$,即$\angle EFD=\frac{1}{2}(\angle C-\angle B)$.
(3)∠EFD与∠C - ∠B的数量关系不会发生变化,$\angle EFD=\frac{1}{2}(\angle C-\angle B)$.理由如下:因为AE平分∠BAC,所以$\angle EAC=\frac{1}{2}\angle BAC=\frac{180^\circ-\angle B-\angle C}{2}=90^\circ-\frac{1}{2}(\angle B+\angle C)$.在△AEC中,$\angle AEC+\angle EAC+\angle C=180^\circ$,所以$\angle AEC=180^\circ-\angle C-\angle EAC=180^\circ-\angle C-90^\circ+\frac{1}{2}(\angle C+\angle B)=90^\circ+\frac{1}{2}(\angle B-\angle C)$,所以$\angle DEF=\angle AEC=90^\circ+\frac{1}{2}(\angle B-\angle C)$.因为FD⊥BC,所以∠FDE=90°,所以$\angle EFD=180^\circ-\angle FDE-\angle DEF=180^\circ-90^\circ-90^\circ-\frac{1}{2}(\angle B-\angle C)$,即$\angle EFD=\frac{1}{2}(\angle C-\angle B)$.