《2025年一遍过八年级数学上册沪科版》

 过中考 中考真题同步挑战 答案 P34
1 [新考法][2024海南中考]设直角三角形中一个锐角为$x度(0 ＜ x ＜ 90)$,另一个锐角为$y$度,则$y与x$的函数关系式为( )

A.$y = 180 + x$
B.$y = 180 - x$
C.$y = 90 + x$
D.$y = 90 - x$

答案： D 由直角三角形的性质得x+y=90,所以y与x的函数关系式为y=90-x.

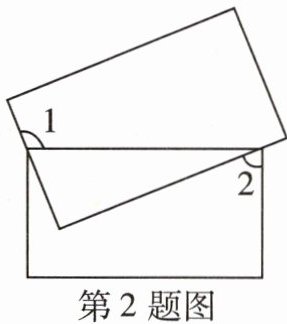
 2 [2022安徽中考]两个长方形的位置如图所示,若$\angle 1 = \alpha$,则$\angle 2 = $( )

A.$\alpha - 90^{\circ}$
B.$\alpha - 45^{\circ}$
C.$180^{\circ} - \alpha$
D.$270^{\circ} - \alpha$

答案： C 如图,∠3=∠1-90°=α-90°,所以∠2=90°-∠3=180°-α.

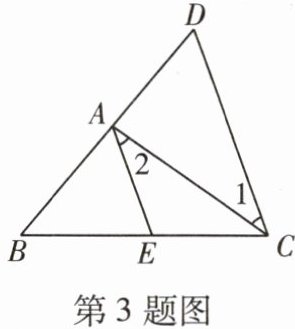
 3 [2023达州中考]如图,$AE// CD$,$CA平分\angle BCD$,$\angle 2 = 35^{\circ}$,$\angle D = 60^{\circ}$,则$\angle B = $( )

A.$52^{\circ}$
B.$50^{\circ}$
C.$45^{\circ}$
D.$25^{\circ}$

答案： B
∵AE//CD,
∴∠1=∠2=35°.
∵CA平分∠BCD,
∴∠BCD=2∠1=70°.又
∵∠D=60°,
∴∠B=180°-∠BCD-∠D=50°.

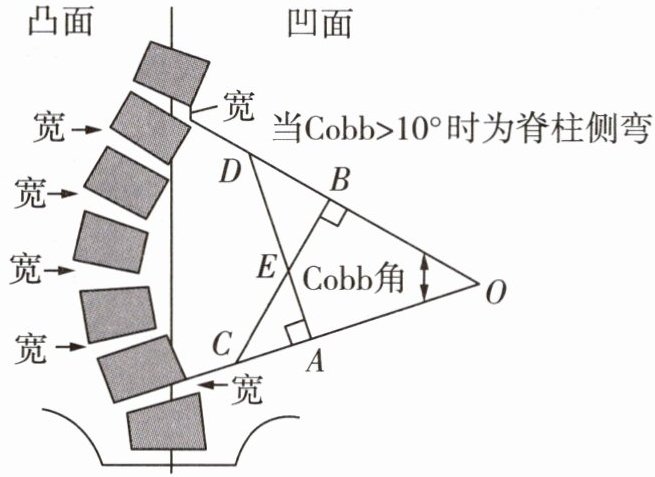
 4 [新情境][2023衢州中考]如图是脊柱侧弯的检测示意图,在体检时为方便测出Cobb角$\angle O$的大小,需将$\angle O$转化为与它相等的角,则图中与$\angle O$相等的角是( )


A.$\angle BEA$
B.$\angle DEB$
C.$\angle ECA$
D.$\angle ADO$

答案： B 由题图可知△DOA和△DBE都是直角三角形,
∴∠O+∠ADO=90°,∠DEB+∠ADO=90°,
∴∠DEB=∠O.

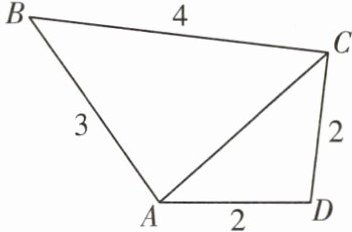
 5 [2023河北中考]四边形$ABCD$的边长如图所示,对角线$AC$的长度随四边形形状的改变而变化.当$\triangle ABC$为等腰三角形时,对角线$AC$的长为( )


A.$2$
B.$3$
C.$4$
D.$5$

答案： B 在△ACD中,AD=CD=2,根据三角形三边关系(三角形任意两边之和大于第三边;任意两边之差小于第三边)可知,0＜AC＜4,
∴当△ABC为等腰三角形时，AC的长为3.

 6 [2024无锡中考]命题“若$a ＞ b$,则$a - 3 ＜ b - 3$”是____命题.(填“真”或“假”)

答案： 假 因为a＞b,所以a-3＞b-3,所以原命题是假命题.

 7 [2022荆门中考]如图,点$G为\triangle ABC$的重心,$D,E,F分别为BC,CA,AB$的中点,具有性质:$AG:GD = BG:GE = CG:GF = 2:1$.已知$\triangle AFG的面积为3$,则$\triangle ABC$的面积为____.

答案： 18
∵CG:GF=2:1,$S_{\triangle AFG}=3$,
∴$S_{\triangle ACG}=6$,
∴$S_{\triangle ACF}=3+6=9$.
∵点F为AB的中点,
∴$S_{\triangle ABC}=2S_{\triangle ACF}=18$.

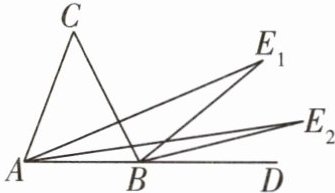
 8 [2024达州中考]如图,在$\triangle ABC$中,$AE_1,BE_1分别是内角\angle CAB$,外角$\angle CBD$的三等分线,且$\angle E_1AD = \frac{1}{3}\angle CAB$,$\angle E_1BD = \frac{1}{3}\angle CBD$,在$\triangle ABE_1$中,$AE_2,BE_2分别是内角\angle E_1AB$,外角$\angle E_1BD$的三等分线,且$\angle E_2AD = \frac{1}{3}\angle E_1AB$,$\angle E_2BD = \frac{1}{3}\angle E_1BD$,……$$,以此规律作下去,若$\angle C = m^{\circ}$,则$\angle E_n = $____度.

答案： $\frac{1}{3^{n}}m$ 因为∠E₁AD=$\frac{1}{3}$∠CAB,∠E₁BD=$\frac{1}{3}$∠CBD,所以设∠E₁AD=α,∠E₁BD=β,则∠CAB=3α,∠CBD=3β,由三角形外角的性质得β=α+∠E₁,3β=3α+∠C,所以∠E₁=$\frac{1}{3}$∠C,同理可得,∠E₂=$\frac{1}{3}$∠E₁,所以∠E₂=$(\frac{1}{3})^{2}$∠C,…,∠Eₙ=$(\frac{1}{3})^{n}$∠C,即∠Eₙ=$\frac{1}{3^{n}}m^{\circ}$.