《2025年一遍过八年级数学上册沪科版》

1 [2025六安期中]三角形的三个内角的度数分别是$70^{\circ },60^{\circ },50^{\circ }$,则这个三角形的形状是( )

A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形

答案： A 三角形的三个内角均为锐角，故这个三角形是锐角三角形.

2 [2025宁波期末]下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形形状的是( )

答案： C A项，露出两个角，由此可得第三个角的度数，故能判断该三角形的形状;B项，露出的角是直角，故该三角形是直角三角形;C项，露出的角是锐角，其他两个角的度数无法确定，故不能判断该三角形的形状;D项，露出的角是钝角，故该三角形是钝角三角形.

3 易错题 如图,在$△ABC$中,$∠BAC=87^{\circ },AD⊥BC$,则图中一共有____个三角形,其中锐角三角形有____个,直角三角形有____个,钝角三角形有____个.

答案： 6 2 3 1 题图中共有6个三角形，其中锐角三角形有2个:△ABE,△ABC;直角三角形有3个:△ABD,△ADE,△ADC;钝角三角形有1个:△AEC.

4 [2025合肥期中]在$△ABC$中,$∠A=60^{\circ },∠B=40^{\circ }$,则$∠C$的度数为( )

A.$100^{\circ }$
B.$80^{\circ }$
C.$60^{\circ }$
D.$40^{\circ }$

答案： B 由三角形的内角和等于180°，得∠C=180°−∠A−∠B=80°.

5 一题多解 [2025池州期末]一个三角形三个内角的度数之比是$2:3:4$,则这个三角形的形状是( )

A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形

答案： A 通解 假设题中所给三角形为△ABC，且∠A:∠B:∠C=2:3:4.设∠A=2x，则∠B=3x，∠C=4x.由题意，知2x+3x+4x=180°，解得x=20°，所以∠A=40°，∠B=60°，∠C=80°，故该三角形是锐角三角形.另解 该三角形最大内角的度数为180°×$\frac{4}{2+3+4}$=80°，故该三角形是锐角三角形.解题通法由角的大小判断三角形形状的方法判断一个三角形的形状，主要看三角形中最大角的度数，若最大角为锐角，则该三角形为锐角三角形;若最大角为直角，则该三角形为直角三角形;若最大角为钝角，则该三角形为钝角三角形.

6 [2024长沙中考]如图,在$△ABC$中,$∠BAC=60^{\circ },∠B=50^{\circ },AD// BC$,则$∠1$的度数为( )

A.$50^{\circ }$
B.$60^{\circ }$
C.$70^{\circ }$
D.$80^{\circ }$

答案： C 因为∠BAC=60°，∠B=50°，所以∠C=180°−∠BAC−∠B=180°−60°−50°=70°.又因为AD//BC，所以∠1=∠C=70°(两直线平行，内错角相等).

7 [2025亳州期中]如图,点E,D分别在AB,AC上,若$∠B=30^{\circ },∠C=55^{\circ }$,则$∠1+∠2$的度数为( )

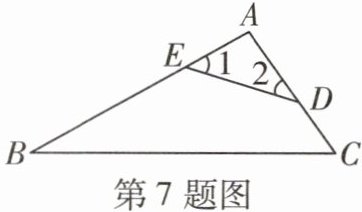
A.$85^{\circ }$
B.$80^{\circ }$
C.$75^{\circ }$
D.$70^{\circ }$

答案： A 因为∠A+∠B+∠C=180°，∠A+∠1+∠2=180°，所以∠1+∠2=∠B+∠C=30°+55°=85°.

8 教材P68T1变式 在$△ABC$中:
(1)若$∠A=80^{\circ },∠B=∠C$,求$∠C$的度数;
(2)若$∠A+∠B=150^{\circ },∠C=3∠A$,求$∠A$的度数;
(3)若$∠B+∠C=2∠A,∠A:∠B=4:5$,求$∠B$的度数.

答案： 解:
(1)∠C=∠B=$\frac{1}{2}$(180°−∠A)=50°.
(2)∠C=180°−(∠A+∠B)=30°，因为∠C=3∠A，所以∠A=$\frac{1}{3}$∠C=10°.
(3)设∠A=4x，则∠B=5x(设参法)，则∠C=180°−∠A−∠B=180°−9x.因为∠B+∠C=2∠A，所以5x+180°−9x=2×4x，解得x=15°，所以∠B=5×15°=75°.

9 一块模板如图所示,规定AF与DE的延长线相交成$70^{\circ }$时,模板合格,但AF与DE的交点不在模板上,不便测量,于是王师傅连接AD,测得$∠FAD=34^{\circ },∠ADE=76^{\circ }$,请你根据这两个角度判断模板是否合格,并说明理由.

答案：
解:模板合格.理由如下:如图,延长AF,DE相交于点O.在△ADO中，因为∠OAD=34°，∠ODA=76°，所以∠AOD=180°−∠OAD−∠ODA=180°−34°−76°=70°，所以模板合格.