第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
过中考 中考真题同步挑战 答案 P47
1 [2024济南中考]如图,已知△ABC≌△DEC,∠A= 60°,∠B= 40°,则∠DCE的度数为( )
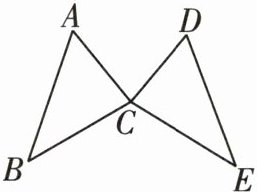
A.40°
B.60°
C.80°
D.100°
1 [2024济南中考]如图,已知△ABC≌△DEC,∠A= 60°,∠B= 40°,则∠DCE的度数为( )

A.40°
B.60°
C.80°
D.100°
答案:
C
∵∠A+∠B+∠ACB=180°,
∴∠ACB=180° - 60° - 40°=80°,
∵△ABC≌△DEC,
∴∠DCE=∠ACB=80°.
∵∠A+∠B+∠ACB=180°,
∴∠ACB=180° - 60° - 40°=80°,
∵△ABC≌△DEC,
∴∠DCE=∠ACB=80°.
2 [2023济宁中考]如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点A,B,C,D,E均在小正方形方格的顶点上,线段AB,CD交于点F,若∠CFB= α,则∠ABE等于( )

A.180°-α
B.180°-2α
C.90°+α
D.90°+2α

A.180°-α
B.180°-2α
C.90°+α
D.90°+2α
答案:
C 如图,易知GE=BC=1,BG=DB=4,∠BGE=∠DBC=∠DBG=90°,
∴△BGE≌△DBC(SAS),
∴∠CDB=∠EBG.
∵∠CFB=∠ABD+∠CDB=α,
∴∠ABE=∠ABD+∠EBG+∠DBG=∠ABD+∠CDB+∠DBG=90°+α.
C 如图,易知GE=BC=1,BG=DB=4,∠BGE=∠DBC=∠DBG=90°,
∴△BGE≌△DBC(SAS),
∴∠CDB=∠EBG.
∵∠CFB=∠ABD+∠CDB=α,
∴∠ABE=∠ABD+∠EBG+∠DBG=∠ABD+∠CDB+∠DBG=90°+α.

3 [2024安徽中考]在凸五边形ABCDE中,AB= AE,BC= DE,F是CD的中点. 下列条件中,不能推出AF与CD一定垂直的是( )
A.∠ABC= ∠AED
B.∠BAF= ∠EAF
C.∠BCF= ∠EDF
D.∠ABD= ∠AEC
A.∠ABC= ∠AED
B.∠BAF= ∠EAF
C.∠BCF= ∠EDF
D.∠ABD= ∠AEC
答案:
D 对于选项A,连接AC,AD,如图1.
∵AB=AE,∠ABC=∠AED,BC=DE,
∴△ABC≌△AED(SAS),
∴AC=AD.又
∵F是AD的中点,
∴CF=DF,又AF=AF,
∴△AFC≌△AFD(SSS),
∴∠AFC=∠AFD,易证∠AFC=∠AFD=90°,
∴AF⊥CD.对于选项B,连接BF,EF,如图2.
∵AB=AE,∠BAF=∠EAF,AF=AF,
∴△ABF≌△AEF(SAS),
∴∠AFB=∠AFE,BF=EF.又
∵BC=DE,CF=DF,
∴△BFC≌△EFD(SSS),
∴∠BFC=∠EFD,
∴∠BFC+∠AFB=∠EFD+∠AFE,即∠AFC=∠AFD=90°,
∴AF⊥CD.对于选项C,如图2,由∠BCF=∠EDF易证△BFC≌△EFD(SAS),
∴∠BFC=∠EFD,BF=EF.又
∵AB=AE,AF=AF,
∴△ABF≌△AEF(SSS),
∴∠AFB=∠AFE,
∴∠BFC+∠AFB=∠EFD+∠AFE,即∠AFC=∠AFD=90°,
∴AF⊥CD.选项D的条件无法证出全等,故证不出AF⊥CD.故选D.

D 对于选项A,连接AC,AD,如图1.
∵AB=AE,∠ABC=∠AED,BC=DE,
∴△ABC≌△AED(SAS),
∴AC=AD.又
∵F是AD的中点,
∴CF=DF,又AF=AF,
∴△AFC≌△AFD(SSS),
∴∠AFC=∠AFD,易证∠AFC=∠AFD=90°,
∴AF⊥CD.对于选项B,连接BF,EF,如图2.
∵AB=AE,∠BAF=∠EAF,AF=AF,
∴△ABF≌△AEF(SAS),
∴∠AFB=∠AFE,BF=EF.又
∵BC=DE,CF=DF,
∴△BFC≌△EFD(SSS),
∴∠BFC=∠EFD,
∴∠BFC+∠AFB=∠EFD+∠AFE,即∠AFC=∠AFD=90°,
∴AF⊥CD.对于选项C,如图2,由∠BCF=∠EDF易证△BFC≌△EFD(SAS),
∴∠BFC=∠EFD,BF=EF.又
∵AB=AE,AF=AF,
∴△ABF≌△AEF(SSS),
∴∠AFB=∠AFE,
∴∠BFC+∠AFB=∠EFD+∠AFE,即∠AFC=∠AFD=90°,
∴AF⊥CD.选项D的条件无法证出全等,故证不出AF⊥CD.故选D.


4 [2023重庆中考A卷]如图,在Rt△ABC中,∠BAC= 90°,AB= AC,点D为BC上一点,连接AD. 过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F. 若BE= 4,CF= 1,则EF的长度为____.


答案:
3
∵BE⊥AD,CF⊥AD,
∴∠BEA=∠AFC=90°,
∴∠BAE+∠ABE=90°.
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠FAC=∠ABE.又AB=AC,
∴△ABE≌△CAF(全等模型——一线三直角),
∴AF=BE=4,AE=CF=1,
∴EF=AF - AE=4 - 1=3.
∵BE⊥AD,CF⊥AD,
∴∠BEA=∠AFC=90°,
∴∠BAE+∠ABE=90°.
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠FAC=∠ABE.又AB=AC,
∴△ABE≌△CAF(全等模型——一线三直角),
∴AF=BE=4,AE=CF=1,
∴EF=AF - AE=4 - 1=3.
5 [2024乐山中考]如图,AB是∠CAD的平分线,AC= AD,求证:∠C= ∠D.


答案:
证明:
∵AB是∠CAD的平分线,
∴∠CAB=∠DAB.
∴在△ABC和△ABD中,AC=AD,∠CAB=∠DAB,AB=AB,
∴△ABC≌△ABD(SAS),
∴∠C=∠D.
∵AB是∠CAD的平分线,
∴∠CAB=∠DAB.
∴在△ABC和△ABD中,AC=AD,∠CAB=∠DAB,AB=AB,
∴△ABC≌△ABD(SAS),
∴∠C=∠D.
6 新趋势·条件开放 [2024淄博中考]如图,已知AB= CD,点E,F在线段BD上,且AF= CE. 请从①BF= DE;②∠BAF= ∠DCE;③AF= CF中选择一个合适的选项作为已知条件,使得△ABF≌△CDE. 你添加的条件是:____(只填写一个序号). 添加条件后,请证明AE//CF.


答案:
①或②,证明如下.当选择①时,证明如下:在△ABF和△CDE中,AB=CD,AF=CE,BF=DE,
∴△ABF≌△CDE(SSS),
∴∠B=∠D,BF=DE,
∴BF+EF=DE+EF,即BE=DF.In△ABE和△CDF中,AB=CD,∠B=∠D,BE=DF,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF.当选择②时,证明如下:在△ABF和△CDE中,AB=CD,∠BAF=∠DCE,AF=CE,
∴△ABF≌△CDE(SAS),
∴∠B=∠D,BF=DE.同理,可证△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF.当选择③时,不能判定△ABF≌△CDE.
∴△ABF≌△CDE(SSS),
∴∠B=∠D,BF=DE,
∴BF+EF=DE+EF,即BE=DF.In△ABE和△CDF中,AB=CD,∠B=∠D,BE=DF,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF.当选择②时,证明如下:在△ABF和△CDE中,AB=CD,∠BAF=∠DCE,AF=CE,
∴△ABF≌△CDE(SAS),
∴∠B=∠D,BF=DE.同理,可证△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF.当选择③时,不能判定△ABF≌△CDE.
查看更多完整答案,请扫码查看


