17. 如图,直线$l是一次函数y = kx + 4$的图象,且直线$l经过点(1,2)$。
(1)求$k$的值;
(2)若直线$l与x$轴、$y轴分别交于A$、$B$两点,求$\triangle AOB$的面积。

(1)求$k$的值;
(2)若直线$l与x$轴、$y轴分别交于A$、$B$两点,求$\triangle AOB$的面积。

答案:
解:
(1)把(1,2)代入$y = kx + 4$,得$k + 4 = 2$.解得$k = - 2$.
(2)当$y = 0$时,$- 2x + 4 = 0$.解得$x = 2$.则直线$y = - 2x + 4$与$x$轴的交点坐标为$A(2,0)$.当$x = 0$时,$y = - 2x + 4 = 4$.则直线$y = - 2x + 4$与$y$轴的交点坐标为$B(0,4)$.所以$S_{\triangle AOB}=\frac{1}{2}×2×4 = 4$.
(1)把(1,2)代入$y = kx + 4$,得$k + 4 = 2$.解得$k = - 2$.
(2)当$y = 0$时,$- 2x + 4 = 0$.解得$x = 2$.则直线$y = - 2x + 4$与$x$轴的交点坐标为$A(2,0)$.当$x = 0$时,$y = - 2x + 4 = 4$.则直线$y = - 2x + 4$与$y$轴的交点坐标为$B(0,4)$.所以$S_{\triangle AOB}=\frac{1}{2}×2×4 = 4$.
18. 为按计划准点到达指定海域,某巡逻艇凌晨$1:00$出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该巡逻艇加快速度仍匀速前进,结果恰好准点到达。如图所示是该巡逻艇行驶的路程$y$(n mile)与所用时间$t$(h)的函数图象,则该巡逻艇原计划准点到达的时刻是几点?
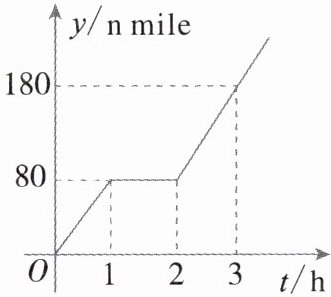

答案:
解:由图象及题意得,故障前的速度为$80÷1 = 80$(n mile/h),故障后的速度为$(180 - 80)÷(3 - 2)=100$(n mile/h).设原计划行驶的时间为$t$h.由题意,得$80t = 80 + 100(t - 2)$.解得$t = 6$.
∴该巡逻艇原计划到达的时刻为$7:00$.
∴该巡逻艇原计划到达的时刻为$7:00$.
查看更多完整答案,请扫码查看


