《2025年湘岳假期暑假作业八年级数学人教版》

7. 将直线$y = x - 1$向上平移2个单位后得到直线$y = kx + b$,则下列关于直线$y = kx + b$的说法正确的是(C)
A.经过第一、第二、第四象限
B.与$x轴交于点(1,0)$
C.与$y轴交于点(0,1)$
D.$y随x$的增大而减小

答案： C

8. 如图,能表示一次函数$y = mx + n与正比例函数y = mnx$($m$,$n$为常数,且$mn \neq 0$)图象的是(D)

答案： D

9. 直线$y = -2x + b$与两坐标轴围成的三角形的面积为4,则$b$的值为(C)
A.4
B.-4
C.$\pm 4$
D.$\pm 2$

答案： C

10. 若$ab ＞ 0$,$bc ＜ 0$,则直线$y = -\frac{a}{b}x - \frac{b}{c}$经过(D)
A.第一、第三、第四象限
B.第一、第二、第三象限
C.第二、第三、第四象限
D.第一、第二、第四象限

答案： D

11. 使函数$y = \sqrt{2x - 1}$有意义的x的取值范围是$x\geqslant\frac{1}{2}$。

答案： $x\geqslant\frac{1}{2}$

12. 直线$y = (2 - 5k)x + 2 - 3k$不过第一象限,则$k$需满足$k\geqslant\frac{2}{3}$,写出一个满足上述条件的函数的解析式：$y = - 3x - 1$。

答案： $k\geqslant\frac{2}{3}$ $y = - 3x - 1$(答案不唯一)

13. 一次函数$y = 2x + 4$的图象经过第一、第二、第三象限,它与$x$轴的交点坐标是(-2,0),与$y$轴的交点坐标是(0,4),$y随x$的增大而增大。

答案： 第一、第二、第三 (-2,0) (0,4) 增大

14. 如图,直线$l是一次函数y = kx + b$的图象,看图填空：
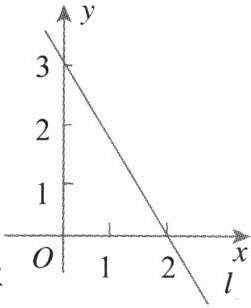
(1)$b = $3,$k = $$-\frac{3}{2}$；
(2)当$x = -20$时,$y = $33；
(3)当$y = -20$时,$x = $$\frac{46}{3}$。

答案：
(1)3 $-\frac{3}{2}$
(2)33
(3)$\frac{46}{3}$

15. 若一次函数$y = x + a$与一次函数$y = -x + b$的图象的交点坐标为$(m,8)$,则$a + b = $16。

答案： 16

16. 如果正比例函数$y = 3x$和一次函数$y = 2x + k$的图象的交点在第三象限,那么$k$的取值范围是$k\lt0$。

答案： $k\lt0$