11. 如图,分别以直角三角形$ABC的斜边AB$,直角边$AC为边向三角形ABC外作等边三角形ABD和等边三角形ACE$.$F为AB$的中点,$DE与AB交于点G$,$EF与AC交于点H$,$\angle ACB= 90^{\circ}$,$\angle BAC= 30^{\circ}$. 给出如下结论:
①$EF\perp AC$;②四边形$ADFE$为菱形;③$AD= 4AG$;④$FH= \frac{1}{4}BD$. 其中正确的有
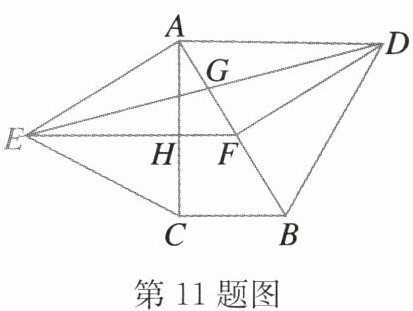
①$EF\perp AC$;②四边形$ADFE$为菱形;③$AD= 4AG$;④$FH= \frac{1}{4}BD$. 其中正确的有
①③④
(填序号).
答案:
①③④
12. 如图,在菱形$ABCD$中,边长为 10,$\angle A= 60^{\circ}$. 顺次连接菱形$ABCD$各边中点,可得四边形$A_{1}B_{1}C_{1}D_{1}$;顺次连接四边形$A_{1}B_{1}C_{1}D_{1}$各边中点,可得四边形$A_{2}B_{2}C_{2}D_{2}$;顺次连接四边形$A_{2}B_{2}C_{2}D_{2}$各边中点,可得四边形$A_{3}B_{3}C_{3}D_{3}……$按此规律继续下去,则四边形$A_{2}B_{2}C_{2}D_{2}$的周长是______
20
;四边形$A_{1000}B_{1000}C_{1000}D_{1000}$的周长是______$\frac{5}{2^{497}}$
.
答案:
20 $ \frac{5}{2^{497}} $
13. 如图,$O是矩形ABCD$对角线的交点,$E$,$F$,$G$,$H分别是OA$,$OB$,$OC$,$OD$上的点,且$AE= BF= CG= DH$.
(1)求证:四边形$EFGH$是矩形;
(2)若$E$,$F$,$G$,$H分别是OA$,$OB$,$OC$,$OD$的中点,且$DG\perp AC$,$OF= 2\mathrm{cm}$,求矩形$ABCD$的面积.
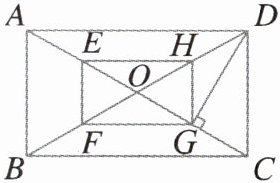
(1)求证:四边形$EFGH$是矩形;
(2)若$E$,$F$,$G$,$H分别是OA$,$OB$,$OC$,$OD$的中点,且$DG\perp AC$,$OF= 2\mathrm{cm}$,求矩形$ABCD$的面积.

答案:
13.
(1)证明:
∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE=BF=CG=DH,
∴AO - AE=OB - BF=CO - CG=DO - DH,即OE=OF=OG=OH.
∴EG=FH.
∴四边形EFGH是矩形.
(2)解:
∵G是OC的中点,
∴GO=GC.
∵DG⊥AC,
∴∠DGO=∠DGC=90°.
∵DG=DG,
∴△DGC≌△DGO(SAS).
∴CD=OD=CO.
∵F是BO的中点,OF = 2cm,
∴BO = 2OF = 4cm.
∵四边形ABCD是矩形,
∴DO = BO = 4cm.
∴DC = 4cm,DB = 8cm.
∴ $CB = \sqrt{DB^2 - DC^2} = \sqrt{8^2 - 4^2} = 4\sqrt{3}(\text{cm})$.
∴ $S_{\text{矩形}ABCD} = 4 × 4\sqrt{3} = 16\sqrt{3} \, (\text{cm}^2)$.
(1)证明:
∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE=BF=CG=DH,
∴AO - AE=OB - BF=CO - CG=DO - DH,即OE=OF=OG=OH.
∴EG=FH.
∴四边形EFGH是矩形.
(2)解:
∵G是OC的中点,
∴GO=GC.
∵DG⊥AC,
∴∠DGO=∠DGC=90°.
∵DG=DG,
∴△DGC≌△DGO(SAS).
∴CD=OD=CO.
∵F是BO的中点,OF = 2cm,
∴BO = 2OF = 4cm.
∵四边形ABCD是矩形,
∴DO = BO = 4cm.
∴DC = 4cm,DB = 8cm.
∴ $CB = \sqrt{DB^2 - DC^2} = \sqrt{8^2 - 4^2} = 4\sqrt{3}(\text{cm})$.
∴ $S_{\text{矩形}ABCD} = 4 × 4\sqrt{3} = 16\sqrt{3} \, (\text{cm}^2)$.
查看更多完整答案,请扫码查看


