16. 如图,正方形 $ABCD$ 的周长为 $16\mathrm{cm}$,顺次连接正方形 $ABCD$ 各边的中点,得到四边形 $EFGH$,则四边形 $EFGH$ 的周长等于
$8\sqrt{2}$
$\mathrm{cm}$,四边形 $EFGH$ 的面积等于 8
$\mathrm{cm}^2$.
答案:
$8\sqrt{2}$ 8
17. 如图,在 $\triangle ABC$ 中,$AB = AC$,$D$,$E$,$F$ 分别是边 $AB$,$BC$,$AC$ 的中点,连接 $DE$,$EF$,要使四边形 $ADEF$ 是正方形,还需增加条件:
$∠A = 90^{\circ}$(答案不唯一)
.
答案:
$∠A = 90^{\circ}$(答案不唯一)
18. 如图,四边形 $ABCD$ 是菱形,对角线 $AC = 8\mathrm{cm}$,$DB = 6\mathrm{cm}$,$DH\perp AB$ 于点 $H$,求 $DH$ 的长.
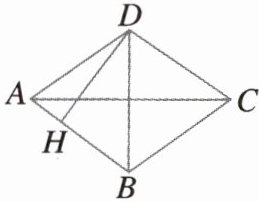

答案:
解:由勾股定理,得
$AB = \sqrt{(\frac{AC}{2})^{2} + (\frac{DB}{2})^{2}} = \sqrt{3^{2} + 4^{2}} = 5(cm)$。
∵$S_{菱形} = \frac{1}{2}AC×BD = AB×DH$,
∴$DH = \frac{1}{2}AC×BD÷AB$
$= \frac{1}{2}×6×8÷5$
$= 4.8(cm)$。
$AB = \sqrt{(\frac{AC}{2})^{2} + (\frac{DB}{2})^{2}} = \sqrt{3^{2} + 4^{2}} = 5(cm)$。
∵$S_{菱形} = \frac{1}{2}AC×BD = AB×DH$,
∴$DH = \frac{1}{2}AC×BD÷AB$
$= \frac{1}{2}×6×8÷5$
$= 4.8(cm)$。
19. 如图,$AD$ 是 $\triangle ABC$ 的中线,$AE// BC$,且 $AE = \frac{1}{2}BC$,连接 $DE$,$CE$.
(1)求证:$AB = DE$;
(2)当 $\triangle ABC$ 满足什么条件时,四边形 $ADCE$ 是矩形?并说明理由.
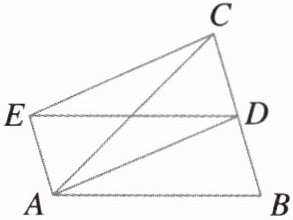
(1)求证:$AB = DE$;
(2)当 $\triangle ABC$ 满足什么条件时,四边形 $ADCE$ 是矩形?并说明理由.

答案:
(1) 证明:
∵AD 是$△ABC$的中线,
∴$BD = CD = \frac{1}{2}BC$。
∵$AE = \frac{1}{2}BC$,
∴$AE = BD$。
∵$AE// BC$,
∴四边形 ABDE 是平行四边形。
∴$AB = DE$。
(2) 解:当$△ABC$满足$AB = AC$时,四边形 ADCE 是矩形。
∵$AE = \frac{1}{2}BC$,$BD = CD = \frac{1}{2}BC$,
∴$AE = CD$。
∵$AE// BC$,
∴四边形 ADCE 是平行四边形。
∵$AB = DE$,
∴当$AB = AC$时,$AC = DE$。
∴平行四边形 ADCE 是矩形。
(1) 证明:
∵AD 是$△ABC$的中线,
∴$BD = CD = \frac{1}{2}BC$。
∵$AE = \frac{1}{2}BC$,
∴$AE = BD$。
∵$AE// BC$,
∴四边形 ABDE 是平行四边形。
∴$AB = DE$。
(2) 解:当$△ABC$满足$AB = AC$时,四边形 ADCE 是矩形。
∵$AE = \frac{1}{2}BC$,$BD = CD = \frac{1}{2}BC$,
∴$AE = CD$。
∵$AE// BC$,
∴四边形 ADCE 是平行四边形。
∵$AB = DE$,
∴当$AB = AC$时,$AC = DE$。
∴平行四边形 ADCE 是矩形。
查看更多完整答案,请扫码查看


