8. 若$\triangle ABC的三边a$,$b$,$c满足a^{2}+b^{2}+c^{2}+50= 6a+8b+10c$,则$\triangle ABC$是(
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
C
)A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
答案:
C
9. 如图,若$\angle BAD= \angle DBC= 90^{\circ}$,$AB= 3$,$AD= 4$,$BC= 12$,则$CD$的长是(
A.12
B.13
C.11
D.15
B
)A.12
B.13
C.11
D.15
答案:
B
10. 以下列各组数为边长,能构成直角三角形的是(
A.$\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$
B.$\sqrt{6}$,$\sqrt{8}$,$\sqrt{10}$
C.$3^{2}$,$4^{2}$,$5^{2}$
D.1,2,3
A
)A.$\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$
B.$\sqrt{6}$,$\sqrt{8}$,$\sqrt{10}$
C.$3^{2}$,$4^{2}$,$5^{2}$
D.1,2,3
答案:
A
11. 在$\triangle ABC$中,$\angle C= 90^{\circ}$,$AB= 7$,$BC= 5$,则边$AC$的长为
2$\sqrt{6}$
。
答案:
2$\sqrt{6}$
12. 如果$\triangle ABC的三边a$,$b$,$c满足关系式|a+2b-60|+(b-18)^{2}+|c-30|= 0$,那么$\triangle ABC$是
直角
三角形。
答案:
直角
13. 如图,圆柱的底面直径为$8cm$,高为$10cm$,一动点$P从点A$出发,沿圆柱的侧面移动到$BD的中点S$的最短距离是______$cm$。($\pi$取3)
13
答案:
13
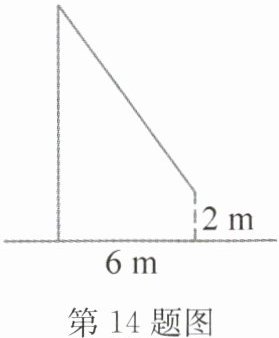
14. 如图,小华将升旗的绳子拉到竖直旗杆的底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆$6m$处,此时绳子末端距离地面$2m$,则绳子的总长度为
10
$m$。
答案:
10
15. 若直角三角形的两直角边长为$a$,$b$,且满足$\sqrt{a^{2}-6a+9}+|b-4|= 0$,则该直角三角形的斜边长为
5
。
答案:
5
16. 在$\triangle ABC$中,$\angle C:\angle B:\angle A= 5:4:1$,则三条边的关系为
$AB^{2}=AC^{2}+BC^{2}$
。
答案:
$AB^{2}=AC^{2}+BC^{2}$
17. 如图,在$\triangle ABC$中,$AB= AC= 10$,$BD\perp AC于点D$,$CD= 2$,则$BC^{2}= $
40
。
答案:
40
查看更多完整答案,请扫码查看


