《2025年快乐假期暑假作业延边教育出版社八年级数学人教版》

12. 如图，在矩形 ABCD 中，$EF// BC$，$GH// AB$，且矩形 AEOH，矩形 HOFD，矩形 OGCF 的面积分别为 9，4，7，则$\triangle HBF$的面积是10.

答案： 10 提示：设$S_{矩形BGOE}=x，$则$S_{△HBF}=S_{矩形ABCD}-S_{△ABH}-S_{△HDF}-S_{△BCF}=9+4+7+x-\frac{1}{2}(9+x)-\frac{1}{2}×4-\frac{1}{2}(7+x)=10.$

13. 如图，在$□ ABCD$中，AC，BD 交于点 O，点 E 为$□ ABCD$外一点，且$∠AEC=∠BED=90^{\circ }$，求证：$□ ABCD$是矩形.

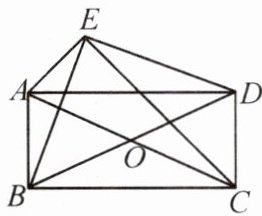
证明：连接OE，设法证AC=BD，从而证得$□ABCD$是矩形.

答案： 提示：连接OE，设法证AC=BD，从而证得
□ABCD是矩形.

14. 如图，在$\triangle ABC$中，点 D 是 BC 边上的一点，点 E 是 AD 的中点，过点 A 作 BC 的平行线交 CE 的延长线于点 F，且$AF=BD$，连接 BF.
（1）求证：点 D 是 BC 的中点；
证明：∵AF//BC，∴∠AFE=∠DCE，∵点 E 是 AD 的中点，∴AE=DE，在△AEF 和△DEC 中，∠AFE=∠DCE，∠AEF=∠DEC，AE=DE，∴△AEF≌△DEC（AAS），∴AF=CD，∵AF=BD，∴CD=BD，即点 D 是 BC 的中点.
（2）如果$AB=AC$，试判断四边形 AFBD 的形状，并证明你的结论.
四边形 AFBD 是矩形，证明：∵AF//BC，AF=BD，∴四边形 AFBD 是平行四边形，∵AB=AC，点 D 是 BC 的中点，∴AD⊥BC，即∠ADB=90°，∴四边形 AFBD 是矩形.

答案： 提示：（1）证△AEF≌△DEC（AAS），由
AF=CD=BD，得D为BC的中点.
（2）四边形AFBD是矩形，设法证∠ADB
=90°，再结合AF=BD，AF//BC，得四边
形AFBD是矩形.