2025年暑假作业与生活陕西师范大学出版总社有限公司八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业与生活陕西师范大学出版总社有限公司八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
24. 如图 1 - 2 - 17,在$Rt\triangle ABC$中,$∠ACB = 90^{\circ}$,$AB = 5cm$,$AC = 3cm$,动点$P从点B出发沿射线BC$以 1 cm/s 的速度移动,设运动的时间为$t$ s。
(1)求$BC$边的长;
(2)当$\triangle ABP$为直角三角形时,求$t$的值;
(3)当$\triangle ABP$为等腰三角形时,求$t$的值。
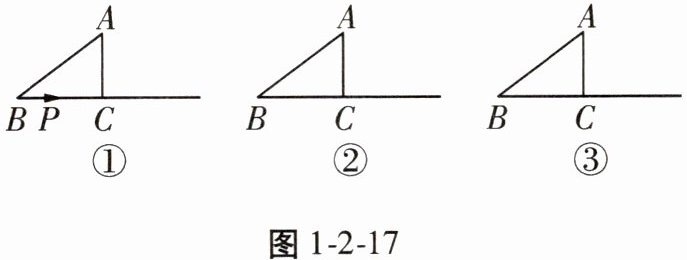
(1)求$BC$边的长;
(2)当$\triangle ABP$为直角三角形时,求$t$的值;
(3)当$\triangle ABP$为等腰三角形时,求$t$的值。

答案:
解:
(1)在$Rt\triangle ABC$中,$BC^{2}=AB^{2}-AC^{2}=5^{2}-3^{2}=16$,
$\therefore BC = 4cm$。
(2)由题意知$BP = tcm$,当$\triangle ABP$为直角三角形时,有两种情况:
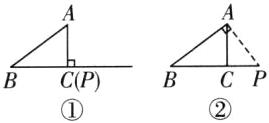
如图①,$\angle APB$为直角时,点$P$与点$C$重合,$BP = BC = 4cm$,即$t = 4$;
如图②,$\angle BAP$为直角时,$BP = tcm$,$CP=(t - 4)cm$,$AC = 3cm$,
在$Rt\triangle ACP$中,$AP^{2}=3^{2}+(t - 4)^{2}$,
在$Rt\triangle BAP$中,$AB^{2}+AP^{2}=BP^{2}$,
即$5^{2}+[3^{2}+(t - 4)^{2}]=t^{2}$,解得$t=\frac{25}{4}$,
故当$\triangle ABP$为直角三角形时,$t = 4$或$t=\frac{25}{4}$。
(3)当$\triangle ABP$为等腰三角形时,有三种情况:
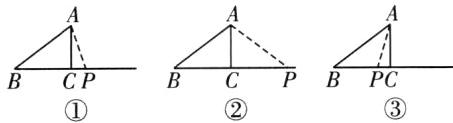
如图①,当$AB = BP$时,$t = 5$;
如图②,当$AB = AP$时,$BP = 2BC = 8cm$,$t = 8$;
如图③,当$BP = AP$时,$AP = BP = tcm$,$CP=(4 - t)cm$,$AC = 3cm$,
在$Rt\triangle ACP$中,$AP^{2}=AC^{2}+CP^{2}$,
所以$t^{2}=3^{2}+(4 - t)^{2}$,解得$t=\frac{25}{8}$。
综上所述,当$\triangle ABP$为等腰三角形时,$t = 5$或$t = 8$或$t=\frac{25}{8}$。
解:
(1)在$Rt\triangle ABC$中,$BC^{2}=AB^{2}-AC^{2}=5^{2}-3^{2}=16$,
$\therefore BC = 4cm$。
(2)由题意知$BP = tcm$,当$\triangle ABP$为直角三角形时,有两种情况:
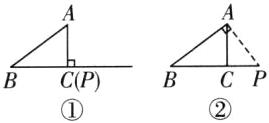
如图①,$\angle APB$为直角时,点$P$与点$C$重合,$BP = BC = 4cm$,即$t = 4$;
如图②,$\angle BAP$为直角时,$BP = tcm$,$CP=(t - 4)cm$,$AC = 3cm$,
在$Rt\triangle ACP$中,$AP^{2}=3^{2}+(t - 4)^{2}$,
在$Rt\triangle BAP$中,$AB^{2}+AP^{2}=BP^{2}$,
即$5^{2}+[3^{2}+(t - 4)^{2}]=t^{2}$,解得$t=\frac{25}{4}$,
故当$\triangle ABP$为直角三角形时,$t = 4$或$t=\frac{25}{4}$。
(3)当$\triangle ABP$为等腰三角形时,有三种情况:

如图①,当$AB = BP$时,$t = 5$;
如图②,当$AB = AP$时,$BP = 2BC = 8cm$,$t = 8$;
如图③,当$BP = AP$时,$AP = BP = tcm$,$CP=(4 - t)cm$,$AC = 3cm$,
在$Rt\triangle ACP$中,$AP^{2}=AC^{2}+CP^{2}$,
所以$t^{2}=3^{2}+(4 - t)^{2}$,解得$t=\frac{25}{8}$。
综上所述,当$\triangle ABP$为等腰三角形时,$t = 5$或$t = 8$或$t=\frac{25}{8}$。
查看更多完整答案,请扫码查看


