《2025年暑假作业与生活陕西师范大学出版总社有限公司八年级数学人教版》

18. 如图 1 - 2 - 11,在$\triangle ABC$中,$∠ACB = 90^{\circ}$,$CD⊥AB$,垂足为$D$,点$E是AB$的中点,若$CD = DE = 2$,求$AB$的长。

答案： 解:$\because$在$Rt\triangle CDE$中,$CD = DE = 2$,
$\therefore CE=\sqrt{CD^{2}+DE^{2}}=2\sqrt{2}$。
$\because$直角三角形斜边上的中线等于斜边的一半,
$\therefore CE=\frac{1}{2}AB$,
$\therefore AB = 2CE = 4\sqrt{2}$。

19. 如图 1 - 2 - 12,在$\triangle ABC$中,已知$AB = AC = 20cm$,$BC = 32cm$,$D是BC$上一点,且$AD⊥AC$,求$BD$的长。

(图1-2-12)

答案：
解:过点$A$作$AE\perp BC$,垂足为$E$。

$\because AB = AC = 20cm$,$BC = 32cm$,
$\therefore CE = BE = 16cm$,
$\therefore$在$Rt\triangle AEC$中,$AE=\sqrt{AC^{2}-EC^{2}}=12cm$。
$\because AD\perp AC$,设$DE = xcm$,
$\therefore$在$Rt\triangle ADC$中,有$AD^{2}=DC^{2}-AC^{2}=(x + 16)^{2}-20^{2}$,
在$Rt\triangle ADE$中,有$AD^{2}=DE^{2}+AE^{2}=x^{2}+12^{2}$,
$\therefore (x + 16)^{2}-20^{2}=x^{2}+12^{2}$,解得$x = 9$,
$\therefore BD = BE - DE = 16 - 9 = 7(cm)$。

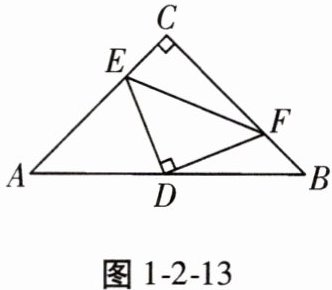
20. 如图 1 - 2 - 13,在$Rt\triangle ABC$中,$∠C = 90^{\circ}$,$D是AB$的中点,$E$,$F分别在AC和BC$上,且$DE⊥DF$。求证：$EF^{2}= AE^{2}+BF^{2}$。

答案：
证明:如图,过点$A$作$AM// BC$,交$FD$的延长线于点$M$,连接$EM$。

$\because AM// BC$,
$\therefore \angle MAE=\angle ACB = 90^{\circ}$,$\angle MAD=\angle B$。
$\because AD = BD$,$\angle ADM=\angle BDF$,
$\therefore \triangle ADM\cong \triangle BDF(ASA)$,
$\therefore AM = BF$,$MD = DF$。
又$\because DE\perp DF$,
$\therefore EF = EM$,
$\therefore AE^{2}+BF^{2}=AE^{2}+AM^{2}=EM^{2}=EF^{2}$。

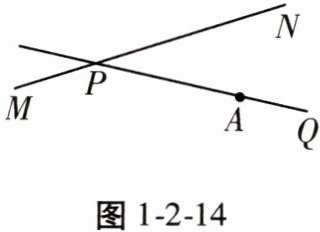
21. 如图 1 - 2 - 14,公路$MN和公路PQ在P$处交汇,且$∠QPN = 30^{\circ}$,在$A$处有一所中学,$AP = 120m$,此时有一辆消防车在公路$MN上沿PN$方向以每秒 5 m 的速度行驶,假设消防车行驶时周围 100 m 以内有噪声影响。
(1)学校是否会受到影响？请说明理由。
(2)如果受到影响,那么影响时间是多长？

答案：
解:
(1)学校会受到噪声影响。理由如下:
如图,作$AB\perp MN$,垂足为$B$,
$\because PA = 120m$,$\angle QPN = 30^{\circ}$,

$\therefore AB=\frac{1}{2}PA = 60m$,而$60m＜100m$,
$\therefore$消防车在公路$MN$上沿$PN$方向行驶时,学校会受到噪声影响。
(2)如图,以点$A$为圆心,$100m$为半径作$\odot A$交$MN$于点$C$和点$D$,
$\because AB\perp CD$,$\therefore CB = BD$。
在$Rt\triangle ABC$中,$AC = 100m$,$AB = 60m$,
$CB=\sqrt{AC^{2}-AB^{2}}=80m$,
$\therefore CD = 2BC = 160m$。
$\because$消防车的速度为$5m/s$,
$\therefore$消防车在线段$CD$上行驶所需要的时间为$160\div 5 = 32(s)$,
$\therefore$学校受影响的时间为$32s$。