12. 某射击队在某次训练中,甲、乙两名队员各射击$10$发子弹,成绩记录如表: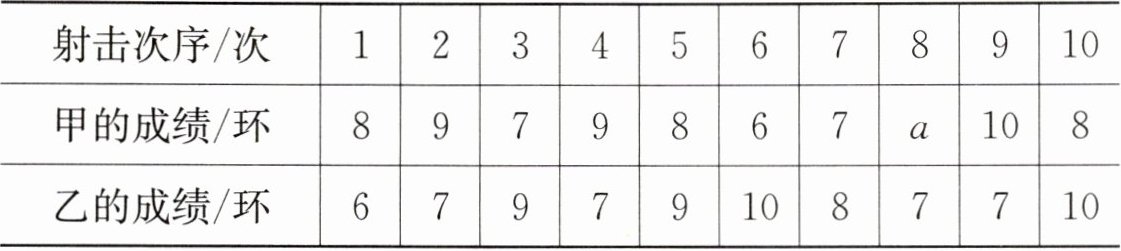
(1)经计算甲和乙的平均成绩都是$8$环,则表中的$a = $____;
(2)甲成绩的中位数是____环,乙成绩的众数是____环;
(3)若甲成绩的方差是$1.2$,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?

(1)经计算甲和乙的平均成绩都是$8$环,则表中的$a = $____;
(2)甲成绩的中位数是____环,乙成绩的众数是____环;
(3)若甲成绩的方差是$1.2$,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?
答案:
【解析】:
### $(1)$求$a$的值
根据平均数公式$\overline{x}=\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}$(其中$\overline{x}$表示平均数,$x_{i}$表示第$i$个数据,$n$表示数据的个数)。
已知甲射击$10$次,平均成绩$\overline{x}_{甲}=8$环,可得$\frac{8 + 9 + 7 + 9 + 8 + 6 + 7 + a + 10 + 8}{10}=8$。
先计算分子:$8 + 9 + 7 + 9 + 8 + 6 + 7 + 10 + 8=72$,则$72 + a = 8×10$,即$72 + a = 80$,解得$a = 8$。
### $(2)$求甲成绩的中位数和乙成绩的众数
**求甲成绩的中位数:**
将甲的成绩从小到大排列为:$6$,$7$,$7$,$8$,$8$,$8$,$8$,$9$,$9$,$10$。
因为$n = 10$(偶数),根据中位数公式$M=\frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$($M$表示中位数),这里$x_{\frac{n}{2}}=x_{5}=8$,$x_{\frac{n}{2}+1}=x_{6}=8$,所以甲成绩的中位数$M=\frac{8 + 8}{2}=8$环。
**求乙成绩的众数:**
众数是一组数据中出现次数最多的数据。
乙的成绩为:$6$,$7$,$9$,$7$,$9$,$10$,$8$,$7$,$7$,$10$,其中$7$出现了$4$次,出现的次数最多,所以乙成绩的众数是$7$环。
### $(3)$求乙成绩的方差并判断谁的成绩更稳定
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\cdots+(x_{n}-\overline{x})^{2}]$。
已知$\overline{x}_{乙}=8$,$n = 10$,$x_{1}=6$,$x_{2}=7$,$x_{3}=9$,$x_{4}=7$,$x_{5}=9$,$x_{6}=10$,$x_{7}=8$,$x_{8}=7$,$x_{9}=7$,$x_{10}=10$。
$\begin{aligned}s_{乙}^{2}&=\frac{1}{10}[(6 - 8)^{2}+4×(7 - 8)^{2}+2×(9 - 8)^{2}+2×(10 - 8)^{2}+(8 - 8)^{2}]\\&=\frac{1}{10}[(- 2)^{2}+4×(-1)^{2}+2×1^{2}+2×2^{2}+0^{2}]\\&=\frac{1}{10}(4 + 4 + 2 + 8)\\&=\frac{1}{10}×18\\&=1.8\end{aligned}$
因为方差越大,表明这组数据波动越大,数据越不稳定;方差越小,表明这组数据波动越小,数据越稳定。
已知$s_{甲}^{2}=1.2$,$s_{乙}^{2}=1.8$,$1.2\lt1.8$,即$s_{甲}^{2}\lt s_{乙}^{2}$,所以甲的成绩更稳定。
【答案】:$(1)8$;$(2)8$,$7$;$(3)$甲
### $(1)$求$a$的值
根据平均数公式$\overline{x}=\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}$(其中$\overline{x}$表示平均数,$x_{i}$表示第$i$个数据,$n$表示数据的个数)。
已知甲射击$10$次,平均成绩$\overline{x}_{甲}=8$环,可得$\frac{8 + 9 + 7 + 9 + 8 + 6 + 7 + a + 10 + 8}{10}=8$。
先计算分子:$8 + 9 + 7 + 9 + 8 + 6 + 7 + 10 + 8=72$,则$72 + a = 8×10$,即$72 + a = 80$,解得$a = 8$。
### $(2)$求甲成绩的中位数和乙成绩的众数
**求甲成绩的中位数:**
将甲的成绩从小到大排列为:$6$,$7$,$7$,$8$,$8$,$8$,$8$,$9$,$9$,$10$。
因为$n = 10$(偶数),根据中位数公式$M=\frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$($M$表示中位数),这里$x_{\frac{n}{2}}=x_{5}=8$,$x_{\frac{n}{2}+1}=x_{6}=8$,所以甲成绩的中位数$M=\frac{8 + 8}{2}=8$环。
**求乙成绩的众数:**
众数是一组数据中出现次数最多的数据。
乙的成绩为:$6$,$7$,$9$,$7$,$9$,$10$,$8$,$7$,$7$,$10$,其中$7$出现了$4$次,出现的次数最多,所以乙成绩的众数是$7$环。
### $(3)$求乙成绩的方差并判断谁的成绩更稳定
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\cdots+(x_{n}-\overline{x})^{2}]$。
已知$\overline{x}_{乙}=8$,$n = 10$,$x_{1}=6$,$x_{2}=7$,$x_{3}=9$,$x_{4}=7$,$x_{5}=9$,$x_{6}=10$,$x_{7}=8$,$x_{8}=7$,$x_{9}=7$,$x_{10}=10$。
$\begin{aligned}s_{乙}^{2}&=\frac{1}{10}[(6 - 8)^{2}+4×(7 - 8)^{2}+2×(9 - 8)^{2}+2×(10 - 8)^{2}+(8 - 8)^{2}]\\&=\frac{1}{10}[(- 2)^{2}+4×(-1)^{2}+2×1^{2}+2×2^{2}+0^{2}]\\&=\frac{1}{10}(4 + 4 + 2 + 8)\\&=\frac{1}{10}×18\\&=1.8\end{aligned}$
因为方差越大,表明这组数据波动越大,数据越不稳定;方差越小,表明这组数据波动越小,数据越稳定。
已知$s_{甲}^{2}=1.2$,$s_{乙}^{2}=1.8$,$1.2\lt1.8$,即$s_{甲}^{2}\lt s_{乙}^{2}$,所以甲的成绩更稳定。
【答案】:$(1)8$;$(2)8$,$7$;$(3)$甲
兄弟俩举行$100\ m$赛跑,当哥哥到达终点时,弟弟才到$95\ m$处,如果让弟弟在原起跑点起跑,哥哥后退$5\ m$跑,兄弟俩的速度仍和原来一样,那么谁将赢得胜利?
分析:设哥哥跑完$100\ m用了t\ s$,在同样时间内弟弟跑完$95\ m$,所以哥哥的速度为$\dfrac{100}{t}\ m/s$,弟弟的速度为$\dfrac{95}{t}\ m/s$. 若哥哥后退$5\ m$起跑,则到达终点需要$\dfrac{100 + 5}{\dfrac{100}{t}}\ s$,弟弟到达终点需要$\dfrac{100}{\dfrac{95}{t}}\ s$,而$\dfrac{100 + 5}{\dfrac{100}{t}}-\dfrac{100}{\dfrac{95}{t}} = (\dfrac{105}{100}-\dfrac{100}{95})t < 0$,所以哥哥到达终点所花时间少,将赢得胜利.
分析:设哥哥跑完$100\ m用了t\ s$,在同样时间内弟弟跑完$95\ m$,所以哥哥的速度为$\dfrac{100}{t}\ m/s$,弟弟的速度为$\dfrac{95}{t}\ m/s$. 若哥哥后退$5\ m$起跑,则到达终点需要$\dfrac{100 + 5}{\dfrac{100}{t}}\ s$,弟弟到达终点需要$\dfrac{100}{\dfrac{95}{t}}\ s$,而$\dfrac{100 + 5}{\dfrac{100}{t}}-\dfrac{100}{\dfrac{95}{t}} = (\dfrac{105}{100}-\dfrac{100}{95})t < 0$,所以哥哥到达终点所花时间少,将赢得胜利.
答案:
【解析】:设哥哥跑完$100m$用了$t s$,根据速度公式$v = \frac{s}{t}$,可得哥哥的速度为$\frac{100}{t}m/s$,弟弟的速度为$\frac{95}{t}m/s$。若哥哥后退$5m$起跑,哥哥跑的路程为$100 + 5 = 105m$,根据时间公式$t=\frac{s}{v}$,则哥哥到达终点需要的时间为$\frac{100 + 5}{\frac{100}{t}}s$;弟弟跑$100m$到达终点需要的时间为$\frac{100}{\frac{95}{t}}s$。计算两者时间差$\frac{100 + 5}{\frac{100}{t}}-\frac{100}{\frac{95}{t}} = (\frac{105}{100}-\frac{100}{95})t$,对$\frac{105}{100}-\frac{100}{95}$通分可得$\frac{105×95 - 100×100}{100×95}=\frac{9975 - 10000}{9500}=-\frac{25}{9500}<0$,所以$(\frac{105}{100}-\frac{100}{95})t< 0$,即哥哥到达终点所花时间少。
【答案】:哥哥
【答案】:哥哥
查看更多完整答案,请扫码查看


