《2025年暑假生活八年级数学人教版北京教育出版社》

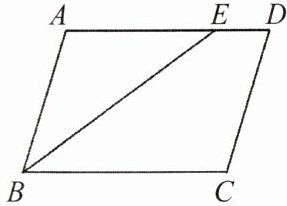
7. 如图,在$□ ABCD$中,$\angle C= 108^{\circ}$,$BE平分\angle ABC$,则$\angle ABE$等于()


A.$108^{\circ}$
B.$72^{\circ}$
C.$36^{\circ}$
D.$18^{\circ}$

答案： C

8. 如图,在$□ ABCD$中,延长$AB到点E$,延长$CD到点F$,使$BE= DF$,连接$AC$,$EF$. 求证：$AC与EF$互相平分.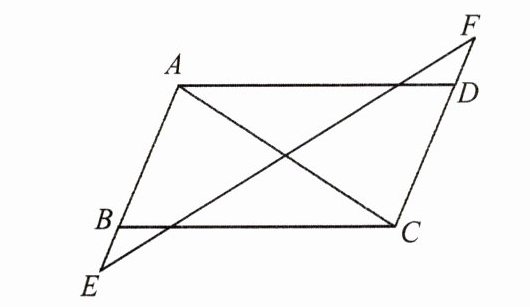

答案： 解：连接$AF$，$CE$。
因为四边形$ABCD$是平行四边形，所以$AB// CD$，$AB = CD$。
又因为$BE = DF$，所以$AB + BE = CD + DF$，即$AE = CF$。
因为$AE// CF$，所以四边形$AECF$是平行四边形（一组对边平行且相等的四边形是平行四边形）。
因为平行四边形的对角线互相平分，所以$AC$与$EF$互相平分。

9. 如图,在$□ ABCD$中,$HE// DA// GF$,若$\angle A= 80^{\circ}$,$AE= 2$,$HG= 1$,$GC= 2$,$AD= 4$.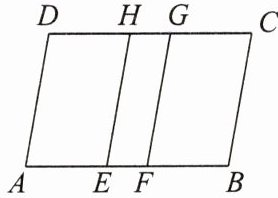
(1)求$\angle GFB及\angle C$的度数.
(2)求$□ ABCD$的周长.

答案：
(1)$∠GFB=80^{\circ },∠C=80^{\circ }$
(2)18