《2025年暑假生活八年级数学人教版北京教育出版社》

8. 如图,在$//ogram ABCD$中,$AC$,$BD相交于点O$,点$E$,$F在对角线AC$上,且$OE= OF$,求证：四边形$EBFD$为平行四边形。

答案： 【解析】：
因为四边形$ABCD$是平行四边形，根据平行四边形的性质：平行四边形的对角线互相平分，所以$OB = OD$。
又已知$OE = OF$，在四边形$EBFD$中，对角线$BD$与$EF$相交于点$O$，且$OB = OD$，$OE = OF$，即四边形$EBFD$的对角线互相平分。
根据平行四边形的判定定理：对角线互相平分的四边形是平行四边形，所以四边形$EBFD$为平行四边形。
【答案】：四边形$EBFD$为平行四边形。

9. 如图,一架云梯$AB$斜靠在墙上,底端$B到墙角C的距离是7m$,若云梯上端下滑$4m到D$处,则底端$B沿水平方向向外滑动8m到E$处,试求云梯$AB$的长度。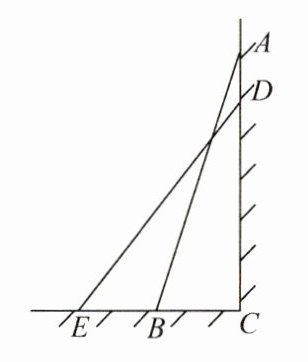

答案： 25 m

10. 某地长途汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定质量,则需要购买行李票。行李票费用$y$(元)是行李质量$x$(千克)的一次函数,其图象如图所示。求：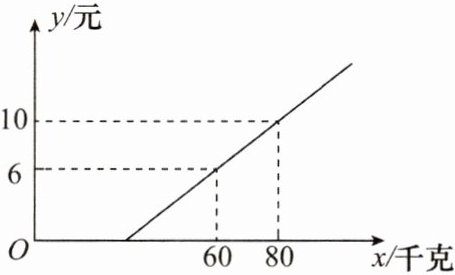
(1)$y与x$之间的函数关系式；
(2)旅客可免费携带行李的最大质量。

答案：
(1) $y=\left\{\begin{array}{l}0,0\lt x\leqslant 30,\\ \frac{1}{5}x - 6,x\gt 30\end{array}\right.$
(2) 30 千克