《2025年暑假生活八年级数学人教版北京教育出版社》

10. 某班同学参加知识竞赛,将成绩进行整理后分成五组,并绘制成如图所示的频数分布直方图,请根据图中的信息,回答问题：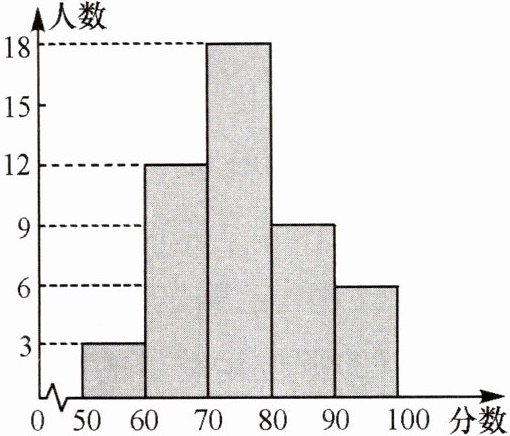
(1)该班共有多少学生参加竞赛?
(2)若80分以上为优秀,则优秀率是多少?
(3)这次竞赛成绩的中位数落在哪个组?
(4)估计该班竞赛成绩的平均分在什么范围.

答案： 【解析】：
(1)将各分数段的人数相加，即$3 + 12 + 18 + 9 + 6 = 48$（人），可得到参加竞赛的学生总数。
(2)先算出$80$分以上（$80 - 90$分和$90 - 100$分）的人数为$9 + 6 = 15$人，再用优秀人数除以总人数乘以$100\%$，即$\frac{15}{48}×100\% = 31.25\%$，得到优秀率。
(3)一共有$48$个数据，中位数是第$24$、$25$个数据的平均数。前两组人数为$3 + 12 = 15$人，前三组人数为$3 + 12 + 18 = 33$人，所以第$24$、$25$个数据在$70 - 80$分数段，即中位数落在$70 - 80$组。
(4)分别计算最低平均分和最高平均分。最低平均分：$\frac{50×3 + 60×12 + 70×18 + 80×9 + 90×6}{48}=\frac{150 + 720 + 1260 + 720 + 540}{48}=\frac{3390}{48} = 70.625$（分）；最高平均分：$\frac{60×3 + 70×12 + 80×18 + 90×9 + 100×6}{48}=\frac{180 + 840 + 1440 + 810 + 600}{48}=\frac{3870}{48} = 80.625$（分），所以平均分在$70.625 - 80.625$范围。
【答案】：
(1)$48$人
(2)$31.25\%$
(3)$70 - 80$组
(4)$70.625 - 80.625$分

11. 为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.

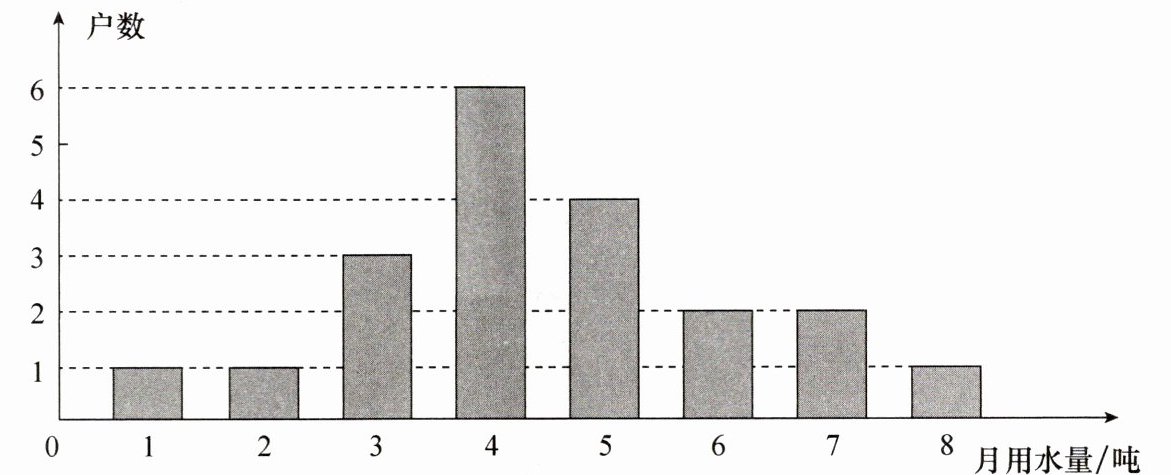
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数、平均数.
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.

答案：
(1)20 户
(2)4 吨 4.5 吨
(3)1 800 吨