9. 如图,矩形 ABCD 的两条对角线相交于点 O,$∠AOD= 120^{\circ },AB= $6 cm,求 AC 的长.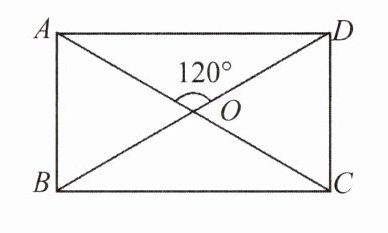

答案:
12 cm
10. 小琼同学在一次班级联欢活动中,用宽度相同的彩带布置教室时,把两种不同颜色的彩带粘贴在一起,发现彩带的重叠部分是一个特殊的四边形(如图). 你知道它是一个怎样的四边形吗? 任意转动这两条彩带,重叠部分仍是这种图形吗? 尝试说明你的判断的正确性.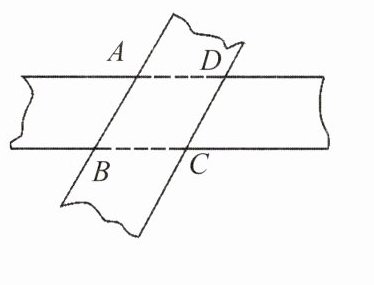

答案:
解:它是一个菱形,任意转动这两条彩带,重叠部分仍是菱形。
理由如下:
因为彩带宽度相同,所以$AB// CD$,$AD// BC$,所以四边形$ABCD$是平行四边形。
分别过点$A$,$C$作$AE\perp BC$于点$E$,$CF\perp AB$于点$F$,因为彩带宽度相同,所以$AE = CF$。
根据平行四边形面积公式$S = 底×高$,可得$S_{//ogram ABCD}=BC\cdot AE = AB\cdot CF$,又因为$AE = CF$,所以$AB = BC$。
根据菱形的判定定理:一组邻边相等的平行四边形是菱形,所以平行四边形$ABCD$是菱形。
由于转动彩带过程中,上述证明条件(对边平行、高相等)始终成立,所以任意转动这两条彩带,重叠部分仍是菱形。
理由如下:
因为彩带宽度相同,所以$AB// CD$,$AD// BC$,所以四边形$ABCD$是平行四边形。
分别过点$A$,$C$作$AE\perp BC$于点$E$,$CF\perp AB$于点$F$,因为彩带宽度相同,所以$AE = CF$。
根据平行四边形面积公式$S = 底×高$,可得$S_{//ogram ABCD}=BC\cdot AE = AB\cdot CF$,又因为$AE = CF$,所以$AB = BC$。
根据菱形的判定定理:一组邻边相等的平行四边形是菱形,所以平行四边形$ABCD$是菱形。
由于转动彩带过程中,上述证明条件(对边平行、高相等)始终成立,所以任意转动这两条彩带,重叠部分仍是菱形。
11. 如图,在正方形 ABCD 中,AC 是对角线,AE 平分$∠BAC,EF⊥AC$于点 F. 求证:$BE= CF.$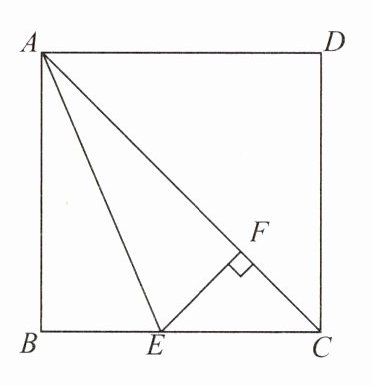

答案:
解:
因为四边形$ABCD$是正方形,所以$\angle B = 90^{\circ}$,$\angle ACB = 45^{\circ}$。
因为$AE$平分$\angle BAC$,$EF\perp AC$,$\angle B = 90^{\circ}$,根据角平分线的性质,角平分线上的点到角两边的距离相等,所以$BE = EF$。
又因为$EF\perp AC$,$\angle ACB = 45^{\circ}$,所以$\triangle EFC$是等腰直角三角形,则$EF = CF$。
因为$BE = EF$,$EF = CF$,所以$BE = CF$。
因为四边形$ABCD$是正方形,所以$\angle B = 90^{\circ}$,$\angle ACB = 45^{\circ}$。
因为$AE$平分$\angle BAC$,$EF\perp AC$,$\angle B = 90^{\circ}$,根据角平分线的性质,角平分线上的点到角两边的距离相等,所以$BE = EF$。
又因为$EF\perp AC$,$\angle ACB = 45^{\circ}$,所以$\triangle EFC$是等腰直角三角形,则$EF = CF$。
因为$BE = EF$,$EF = CF$,所以$BE = CF$。
查看更多完整答案,请扫码查看


