《2025年暑假生活八年级数学人教版北京教育出版社》

13. 细心观察图,解答问题.
(1)求出$OA_{10}^{2}$的值.
(2)请用含有n(n是正整数)的代数式表示$OA_{n}^{2}$.
(3)求出$OA_{1}^{2}+OA_{2}^{2}+OA_{3}^{2}+…+OA_{n}^{2}$的值.

答案： 【解析】：
(1)
已知$OA_{1}^{2}=1^{2}=1$，$OA_{2}^{2}=1^{2}+1^{2}=2$，$OA_{3}^{2}=1^{2}+OA_{2}^{2}=1 + 2 = 3$，$OA_{4}^{2}=1^{2}+OA_{3}^{2}=1 + 3 = 4$，依此类推，可得$OA_{n}^{2}=n$。
所以$OA_{10}^{2}=10$。
(2)
由
(1)的推理过程可知$OA_{n}^{2}=n$（$n$是正整数）。
(3)
$OA_{1}^{2}+OA_{2}^{2}+OA_{3}^{2}+\cdots+OA_{n}^{2}=1 + 2 + 3+\cdots + n$。
根据等差数列求和公式$S_n=\frac{n(a_1 + a_n)}{2}$（这里$a_1 = 1$，$a_n = n$），可得$1 + 2 + 3+\cdots + n=\frac{n(n + 1)}{2}$。
【答案】：
(1)$10$
(2)$n$
(3)$\frac{n(n + 1)}{2}$

勾股定理与三角形三边的关系
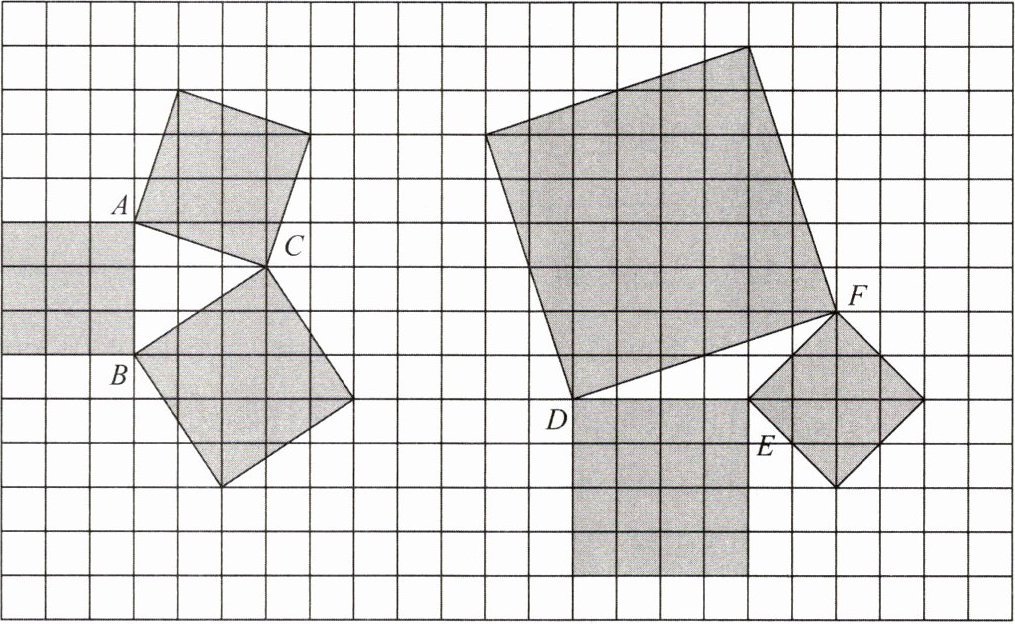
观察图中的△ABC和△DEF,并分别以锐角三角形ABC和钝角三角形DEF的各边为边向外作正方形,探究两个小正方形面积的和与大正方形面积的关系,请结合勾股定理说一说锐角、钝角和直角三角形三边长的平方之间的关系.

答案： 解：设直角三角形三边为$a$、$b$（两直角边）、$c$（斜边），根据勾股定理有$a^{2}+b^{2}=c^{2}$。
设锐角三角形三边为$m$、$n$、$p$（$p$为最长边），通过观察图中以锐角三角形三边向外作正方形，可得$m^{2}+n^{2}＞p^{2}$。
设钝角三角形三边为$x$、$y$、$z$（$z$为最长边），通过观察图中以钝角三角形三边向外作正方形，可得$x^{2}+y^{2}＜z^{2}$。
综上，直角三角形三边$a$、$b$、$c$（$c$为斜边）满足$a^{2}+b^{2}=c^{2}$；锐角三角形三边$m$、$n$、$p$（$p$为最长边）满足$m^{2}+n^{2}＞p^{2}$；钝角三角形三边$x$、$y$、$z$（$z$为最长边）满足$x^{2}+y^{2}＜z^{2}$。