《2025年暑假生活八年级数学人教版北京教育出版社》

9. 某果园有果树200棵,从中随机抽取5棵,每棵果树的产量(单位:千克)如下:98,102,97,103,105.
(1)求这5棵果树的平均产量和产量的中位数.
(2)估计这200棵果树的总产量.

答案：
(1)平均产量是 101 千克，产量的中位数是 102 千克
(2)20 200 千克

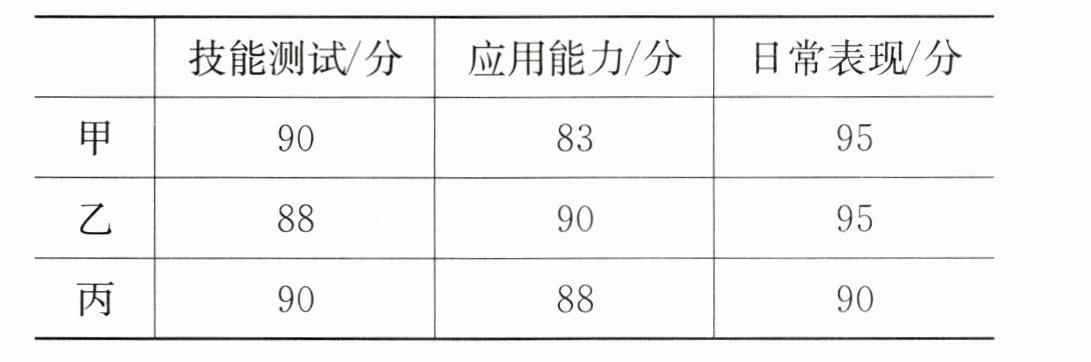
10. 某公司把新入职员工实习期的技能测试、应用能力、日常表现三项成绩分别按50%,20%,30%的比例计入实习期综合测试成绩,90分以上为优秀,甲、乙、丙三人的各项成绩如下表,谁的实习期综合测试成绩为优秀?请说明理由.

答案： 【解析】：本题可根据加权平均数公式分别计算出甲、乙、丙三人的实习期综合测试成绩，再与$90$分比较，判断谁的成绩为优秀。
加权平均数公式为$\overline{x}=w_1x_1 + w_2x_2 + \cdots + w_nx_n$（其中$w_1,w_2,\cdots,w_n$为各数据的权重，$x_1,x_2,\cdots,x_n$为各数据）。
- **计算甲的实习期综合测试成绩：**
已知技能测试、应用能力、日常表现三项成绩分别按$50\%$，$20\%$，$30\%$的比例计入综合测试成绩，甲的技能测试成绩为$85$分，应用能力成绩为$90$分，日常表现成绩为$92$分。
根据加权平均数公式可得甲的综合测试成绩为：
$85×50\% + 90×20\% + 92×30\%$
$= 42.5 + 18 + 27.6$
$= 88.1$（分）
- **计算乙的实习期综合测试成绩：**
乙的技能测试成绩为$92$分，应用能力成绩为$85$分，日常表现成绩为$90$分。
同理可得乙的综合测试成绩为：
$92×50\% + 85×20\% + 90×30\%$
$= 46 + 17 + 27$
$= 90$（分）
- **计算丙的实习期综合测试成绩：**
丙的技能测试成绩为$90$分，应用能力成绩为$92$分，日常表现成绩为$85$分。
则丙的综合测试成绩为：
$90×50\% + 92×20\% + 85×30\%$
$= 45 + 18.4 + 25.5$
$= 88.9$（分）
因为$90$分以上为优秀，$88.1\lt 90$，$90 = 90$，$88.9\lt 90$，所以只有乙的成绩达到优秀标准。
【答案】：乙的实习期综合测试成绩为优秀，理由：甲的综合测试成绩为$88.1$分，乙的综合测试成绩为$90$分，丙的综合测试成绩为$88.9$分，因为$90$分以上为优秀，所以只有乙的成绩达到优秀标准。

11. 某风景区对5个旅游景点的门票价格进行调整,据统计,调价前后各景点的游客人数基本不变,有关数据如下表所示:

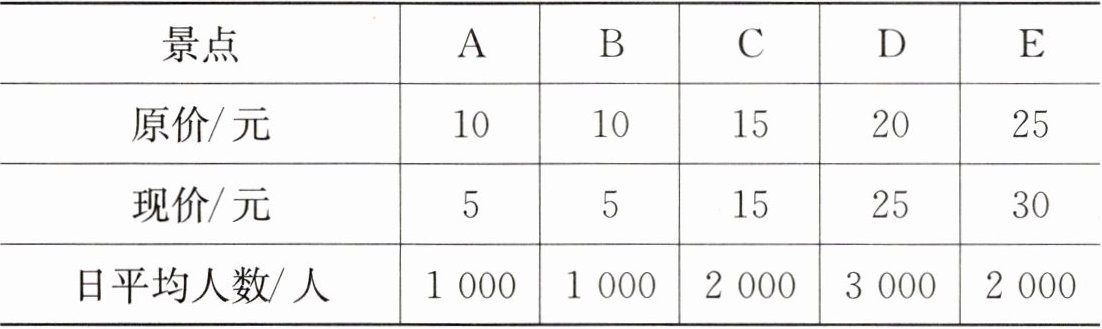
(1)该风景区称调整前后这5个景点门票的平均收费不变,日平均总收入持平,风景区是怎样计算的?
(2)另一方面,游客认为调整收费后风景区的日平均总收入相对于调价前,实际增加了9.4%,问:游客是怎样计算的?
(3)你认为风景区和游客哪个说法较能反映实际情形?

答案： 【解析】：
(1)风景区计算调整前的平均价格：$(10 + 10 + 15 + 20 + 25)÷5 = 16$（元），调整后的平均价格：$(5 + 5 + 15 + 25 + 30)÷5 = 16$（元）。因为平均价格不变，且日平均人数不变，所以认为日平均总收入持平（日平均总收入$=$平均价格$×$日平均总人数）。
(2)游客计算调整前的日平均总收入：$10×1000 + 10×1000 + 15×2000 + 20×3000 + 25×2000$
$=10000 + 10000 + 30000 + 60000 + 50000 = 160000$（元）；
调整后的日平均总收入：$5×1000 + 5×1000 + 15×2000 + 25×3000 + 30×2000$
$=5000 + 5000 + 30000 + 75000 + 60000 = 175000$（元）；
则$(175000 - 160000)÷160000×100\% = 9.4\%$（保留一位小数）。
(3)游客的说法较能反映实际情形，因为虽然平均价格不变，但是各景点价格调整幅度不同，且不同价格景点的日平均人数不同，不能简单用平均价格判断总收入变化，游客根据实际的日平均总收入计算更能反映实际。
【答案】：
(1)风景区通过计算调整前后门票的平均价格（均为$16$元），结合日平均人数不变，认为日平均总收入持平。
(2)游客通过分别计算调整前后的日平均总收入（调整前$160000$元，调整后$175000$元），再计算增加比例$(175000 - 160000)÷160000×100\%\approx9.4\%$。
(3)游客。