8. 如图,在菱形$ABCD$中,$E$,$F分别是BC$,$CD$上的点,且$AE= EF= AF= BC$.求$∠C$的度数.

答案:
$100^{\circ}$
9. 如图,$//ogram ABCD的对角线AC的垂直平分线与边AD$,$BC分别相交于点E$,$F$,$AC与EF交于点O$,连接$AF$,$CE$.求证:四边形$AFCE$是菱形.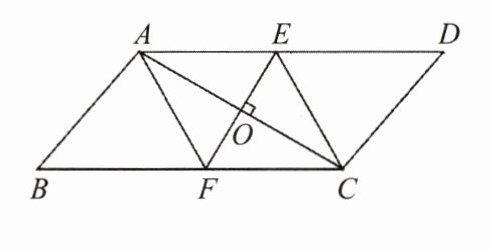

答案:
【解析】:
1. 首先,根据平行四边形的性质:
因为四边形$ABCD$是平行四边形,所以$AD// BC$,根据两直线平行内错角相等,可得$\angle EAO=\angle FCO$。
2. 然后,证明$\triangle AOE\cong\triangle COF$:
已知$EF$是$AC$的垂直平分线,所以$AO = CO$,$\angle AOE=\angle COF = 90^{\circ}$。
在$\triangle AOE$和$\triangle COF$中,$\begin{cases}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{cases}$,根据“角 - 边 - 角”($ASA$)全等判定定理,可得$\triangle AOE\cong\triangle COF$。
由全等三角形的性质可知$OE = OF$。
3. 接着,根据平行四边形的判定定理:
因为$AO = CO$,$OE = OF$,根据“对角线互相平分的四边形是平行四边形”,所以四边形$AFCE$是平行四边形。
4. 最后,根据菱形的判定定理:
又因为$EF\perp AC$,即平行四边形$AFCE$的对角线互相垂直,根据“对角线互相垂直的平行四边形是菱形”,所以四边形$AFCE$是菱形。
【答案】:四边形$AFCE$是菱形。
1. 首先,根据平行四边形的性质:
因为四边形$ABCD$是平行四边形,所以$AD// BC$,根据两直线平行内错角相等,可得$\angle EAO=\angle FCO$。
2. 然后,证明$\triangle AOE\cong\triangle COF$:
已知$EF$是$AC$的垂直平分线,所以$AO = CO$,$\angle AOE=\angle COF = 90^{\circ}$。
在$\triangle AOE$和$\triangle COF$中,$\begin{cases}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{cases}$,根据“角 - 边 - 角”($ASA$)全等判定定理,可得$\triangle AOE\cong\triangle COF$。
由全等三角形的性质可知$OE = OF$。
3. 接着,根据平行四边形的判定定理:
因为$AO = CO$,$OE = OF$,根据“对角线互相平分的四边形是平行四边形”,所以四边形$AFCE$是平行四边形。
4. 最后,根据菱形的判定定理:
又因为$EF\perp AC$,即平行四边形$AFCE$的对角线互相垂直,根据“对角线互相垂直的平行四边形是菱形”,所以四边形$AFCE$是菱形。
【答案】:四边形$AFCE$是菱形。
10. 如图,在$△ABC$中,$∠ACB= 90^{\circ}$,$CD平分∠ACB$,$DE⊥BC$,$DF⊥AC$,垂足分别为$E$,$F$,试说明四边形$CEDF$是正方形.
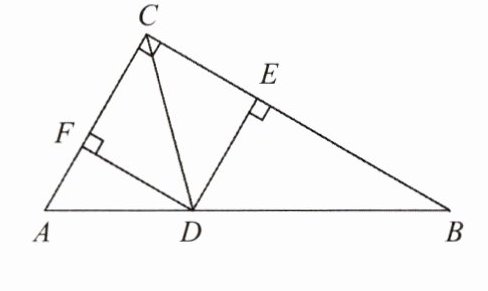

答案:
【解析】:本题可根据已知条件,先证明四边形$CEDF$是矩形,再证明其一组邻边相等,进而得出四边形$CEDF$是正方形。
**步骤一:证明四边形$CEDF$是矩形**
已知$\angle ACB = 90^{\circ}$,$DE\perp BC$,$DF\perp AC$,则$\angle DEC = \angle DFC = \angle ACB = 90^{\circ}$。
根据四边形的内角和为$360^{\circ}$,可得$\angle EDF = 360^{\circ} - \angle DEC - \angle DFC - \angle ACB = 360^{\circ} - 90^{\circ} - 90^{\circ} - 90^{\circ} = 90^{\circ}$。
因为四边形$CEDF$的四个角都是直角,所以四边形$CEDF$是矩形。
**步骤二:证明矩形$CEDF$的一组邻边相等**
因为$CD$平分$\angle ACB$,$DE\perp BC$,$DF\perp AC$,根据角平分线的性质:角平分线上的点到角两边的距离相等,可得$DF = DE$。
**步骤三:根据正方形的判定定理得出结论**
一组邻边相等的矩形是正方形,由于四边形$CEDF$是矩形且$DF = DE$,所以四边形$CEDF$是正方形。
【答案】:因为$\angle ACB = 90^{\circ}$,$DE\perp BC$,$DF\perp AC$,所以$\angle DEC = \angle DFC = \angle ACB = 90^{\circ}$,则四边形$CEDF$是矩形。又因为$CD$平分$\angle ACB$,$DE\perp BC$,$DF\perp AC$,所以$DF = DE$,所以矩形$CEDF$是正方形。
**步骤一:证明四边形$CEDF$是矩形**
已知$\angle ACB = 90^{\circ}$,$DE\perp BC$,$DF\perp AC$,则$\angle DEC = \angle DFC = \angle ACB = 90^{\circ}$。
根据四边形的内角和为$360^{\circ}$,可得$\angle EDF = 360^{\circ} - \angle DEC - \angle DFC - \angle ACB = 360^{\circ} - 90^{\circ} - 90^{\circ} - 90^{\circ} = 90^{\circ}$。
因为四边形$CEDF$的四个角都是直角,所以四边形$CEDF$是矩形。
**步骤二:证明矩形$CEDF$的一组邻边相等**
因为$CD$平分$\angle ACB$,$DE\perp BC$,$DF\perp AC$,根据角平分线的性质:角平分线上的点到角两边的距离相等,可得$DF = DE$。
**步骤三:根据正方形的判定定理得出结论**
一组邻边相等的矩形是正方形,由于四边形$CEDF$是矩形且$DF = DE$,所以四边形$CEDF$是正方形。
【答案】:因为$\angle ACB = 90^{\circ}$,$DE\perp BC$,$DF\perp AC$,所以$\angle DEC = \angle DFC = \angle ACB = 90^{\circ}$,则四边形$CEDF$是矩形。又因为$CD$平分$\angle ACB$,$DE\perp BC$,$DF\perp AC$,所以$DF = DE$,所以矩形$CEDF$是正方形。
查看更多完整答案,请扫码查看


