《2025年暑假作业与生活八年级数学北师大版陕西师范大学出版总社有限公司》

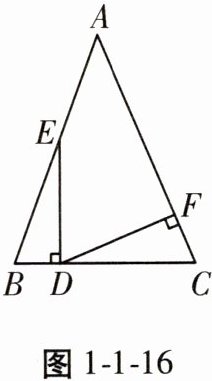
19. 如图1-1-16,在$△ABC$中,D是BC边上的一点,$DE⊥BC$,交AB边于点E,$DF⊥AC$,垂足为F,$BE= CD,BD= CF$。
(1)求证：$△ABC$是等腰三角形；
(2)连接EF,当$∠A$为多少度时,$△DEF$是等边三角形？请说明理由。

答案：

(1) 证明:
∵DE⊥BC，DF⊥AC，
∴∠BDE = 90°，∠DFC = 90°。
在Rt△BDE和Rt△CFD中，
$\left\{ \begin{array} { l } { BE = CD, } \\ { BD = CF, } \end{array} \right.$
∴Rt△BDE ≌ Rt△CFD，
∴∠B = ∠C，
∴△ABC是等腰三角形。
(2) 解:如图所示。
∵Rt△BDE ≌ Rt△CFD，
∴DE = DF。

当△DEF是等边三角形时，∠EDF = 60°，
∴∠CDF = 90° - ∠EDF = 30°，
∴∠C = 90° - ∠CDF = 60°，
∴∠B = ∠C = 60°，
∴∠A = 180° - ∠B - ∠C = 60°，
∴当∠A = 60°时，△DEF是等边三角形。

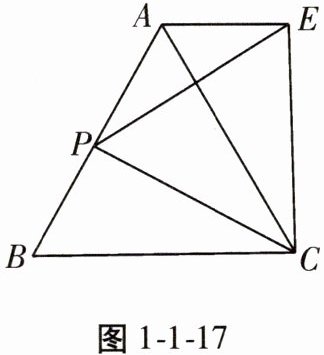
20. 如图1-1-17,$△ABC$为等边三角形,点P在边AB上,以CP为一边作等边三角形PCE。求证：$AE// BC$。

答案： 证明:
∵△ABC，△PCE均为等边三角形，
∴∠ACB = ∠ABC = ∠PCE = 60°，
∴∠ACB - ∠ACP = ∠PCE - ∠ACP，
即∠BCP = ∠ACE。
在△BCP和△ACE中，
$\left\{ \begin{array} { l } { BC = AC, } \\ { ∠BCP = ∠ACE, } \\ { PC = EC, } \end{array} \right.$
∴△BCP ≌ △ACE，
∴∠CBP = ∠CAE = 60°，
∴∠CAE = ∠ACB，
∴AE // BC。

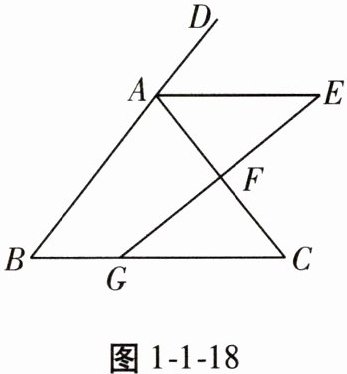
21. 如图1-1-18,在$△ABC$中,点D在线段BA的延长线上,过AC的中点F作线段GE交$∠DAC$的平分线于点E,交BC于点G,且$AE// BC$。若$AE= 8,AB= 10,GC= 2BG$,求$△ABC$的周长。

答案： 解:
∵AE // BC，
∴∠B = ∠DAE，∠C = ∠CAE。
∵AE平分∠DAC，
∴∠DAE = ∠CAE，
∴∠B = ∠C，
∴AB = AC = 10。
∵F是AC的中点，
∴AF = CF。
在△AFE和△CFG中，
$\left\{ \begin{array} { l } { ∠FAE = ∠C, } \\ { AF = CF, } \\ { ∠AFE = ∠GFC, } \end{array} \right.$
∴△AFE ≌ △CFG，
∴AE = GC = 8。
∵GC = 2BG，
∴BG = 4，
∴BC = 12，
∴△ABC的周长为AB + AC + BC = 10 + 10 + 12 = 32。