2. 小明买了一块等腰三角形的蛋糕,他打算将这块蛋糕做成平行四边形形状后送给小强。小明只切了一刀,便拼出了一个平行四边形,且蛋糕没有浪费。
(1)你知道小明是怎样切的吗?用虚线在图1-7-2中表示出刀痕;
(2)请你画出小明所拼的平行四边形。

(1)你知道小明是怎样切的吗?用虚线在图1-7-2中表示出刀痕;
(2)请你画出小明所拼的平行四边形。

答案:
答案不唯一。分析:可利用三角形中位线的性质或等腰三角形底边上的中线割补拼成平行四边形。
1. 若▱ABCD的周长为40 cm,$\triangle ABC$的周长为25 cm,则对角线AC的长是()
A. 5 cm
B. 15 cm
C. 6 cm
D. 16 cm
A. 5 cm
B. 15 cm
C. 6 cm
D. 16 cm
答案:
A
2. 下列条件不能判定四边形是平行四边形的是()
A. 一组对边平行且相等
B. 两组对边分别相等
C. 一组对边平行,另一组对边相等
D. 两组对角分别相等
A. 一组对边平行且相等
B. 两组对边分别相等
C. 一组对边平行,另一组对边相等
D. 两组对角分别相等
答案:
C
3. 如图1-7-3,在▱ABCD中,若$AB= 6,AD= 4,∠B= 150^{\circ }$,则$//ogram ABCD$的面积为()
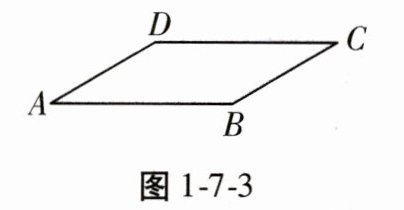
A. 6
B. 12
C. $12\sqrt {3}$
D. 24

A. 6
B. 12
C. $12\sqrt {3}$
D. 24
答案:
B
4. 如图1-7-4,在▱ABCD中,对角线AC,BD交于点O,过点O的直线分别交AD,BC于点E,F,则图中全等的三角形共有()
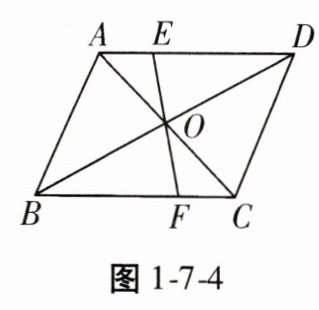
A. 2对
B. 4对
C. 6对
D. 8对

A. 2对
B. 4对
C. 6对
D. 8对
答案:
C
5. 如图1-7-5,在▱ABCD中,不一定成立的是()
①$AO= CO$;②$AC⊥BD$;③$AD// BC$;④$∠CAB= ∠CAD$。
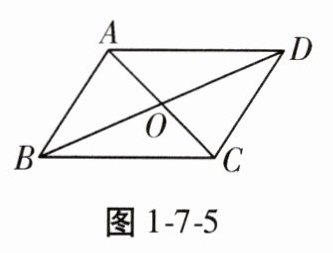
A. ①③
B. ②③
C. ③④
D. ②④
①$AO= CO$;②$AC⊥BD$;③$AD// BC$;④$∠CAB= ∠CAD$。

A. ①③
B. ②③
C. ③④
D. ②④
答案:
D
查看更多完整答案,请扫码查看


