8. 一个多边形的内角和是外角和的3倍,则这个多边形是 ()
A. 六边形
B. 七边形
C. 八边形
D. 九边形
A. 六边形
B. 七边形
C. 八边形
D. 九边形
答案:
C
9. 如图2-2-3,在$\triangle ABC$中,$∠C= 60^{\circ }$,若沿图中虚线截去$∠C$,则$∠1+∠2$等于 ()
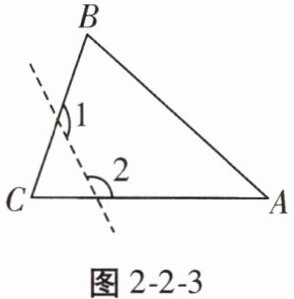
A. $360^{\circ }$
B. $240^{\circ }$
C. $180^{\circ }$
D. $140^{\circ }$

A. $360^{\circ }$
B. $240^{\circ }$
C. $180^{\circ }$
D. $140^{\circ }$
答案:
B
10. 如图2-2-4,DE是$\triangle ABC$的中位线,点F在DE上,且$∠AFC= 90^{\circ }$。若$AC= 10$,$BC= 16$,则DF的长为 ()
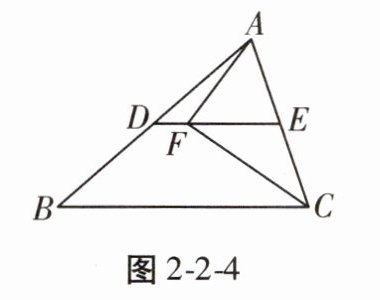
A. 5
B. 3
C. 8
D. 10

A. 5
B. 3
C. 8
D. 10
答案:
B
11. 因式分解:$2m^{3}-8m= $____。
答案:
$2m(m + 2)(m - 2)$
12. 如图2-2-5,▱ABCD的对角线AC,BD相交于点O,点E是AB的中点,$\triangle AEO$的周长是8,则$\triangle ACD$的周长为____。
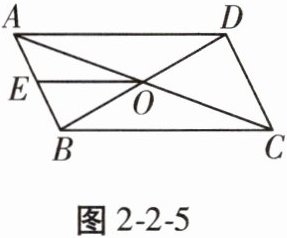

答案:
16
13. 已知关于x的分式方程$\frac {x-3}{x-2}= 2-\frac {m}{2-x}$有增根,则$m= $____。
答案:
-1
14. 如果$\triangle ABC$的顶点A的坐标为$(1,2)$,经过平移后的对应点$A'的坐标为(-1,3)$,那么顶点$B(-2,1)平移后的对应点B'$的坐标为____。
答案:
$( - 4, 2)$
15. 如图2-2-6,在四边形ABCD中,$AB= AD,∠BAD= ∠BCD= 90^{\circ }$,连接AC。若$AC= 6$,则四边形ABCD的面积为____。
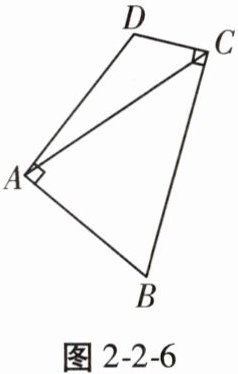

答案:
18
16. (8分)化简。
(1)$\frac {x}{x^{2}-1}÷\frac {1}{x-1}$; (2)$(\frac {a-2}{a+2}+\frac {8a}{a^{2}-4})÷\frac {a+2}{a^{2}-2a}$。
(1)$\frac {x}{x^{2}-1}÷\frac {1}{x-1}$; (2)$(\frac {a-2}{a+2}+\frac {8a}{a^{2}-4})÷\frac {a+2}{a^{2}-2a}$。
答案:
(1) $\frac{x}{x + 1}$
(2) $a$
(1) $\frac{x}{x + 1}$
(2) $a$
查看更多完整答案,请扫码查看


