《2025年暑假作业与生活八年级数学北师大版陕西师范大学出版总社有限公司》

22. (8分)如图2-1-10,以BC为底边的等腰三角形ABC,点D,E,G分别在BC,AB,AC上,且$EG// BC,DE// AC$,延长GE至点F,使得$BE= BF$。求证:四边形BDEF为平行四边形。

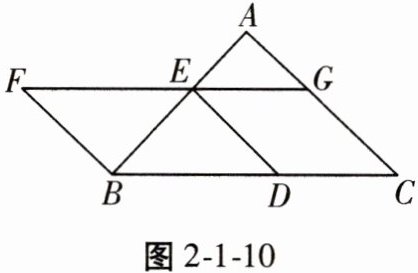
答案： 证明:
∵△ABC是等腰三角形,
∴∠ABC = ∠C。
∵EG//BC,DE//AC,
∴∠AEG = ∠ABC = ∠C,四边形CDEG是平行四边形,
∴∠DEG = ∠C。
∵BE = BF,
∴∠F = ∠BEF = ∠AEG = ∠ABC,
∴∠F = ∠DEG,
∴BF//DE,
∴四边形BDEF为平行四边形。

23. (12分)某市始终践行国家关于“积极稳妥推进碳达峰碳中和”的战略布署,计划购买A型和B型两种环保节能公交车共10辆。若购买A型公交车2辆,B型公交车3辆,共需750万元;若购买A型公交车3辆,B型公交车4辆,共需1040万元。
(1)求购买A型和B型公交车每辆各需多少万元;
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次。若该公司购买A型和B型公交车的总费用不超过1550万元,且确保这10辆公交车在该线路的年均载客总和不少于720万人次,则该公司有几种购车方案? 哪种购车方案总费用最少?最少总费用是多少万元?

答案： 解:
(1) 设购买A型公交车每辆需x万元,B型公交车每辆需y万元。
由题意,得$\begin{cases}2x + 3y = 750, \\3x + 4y = 1040, \end{cases}$
解得$\begin{cases}x = 120, \\y = 170, \end{cases}$
∴购买A型公交车每辆需120万元,B型公交车每辆需170万元。
(2) 设购买A型m辆,B型(10 - m)辆。
由题意,得$\begin{cases}120m + 170(10 - m) \leq 1550, \\60m + 100(10 - m) \geq 720, \end{cases}$
∴3≤m≤7,
且m为自然数,
∴m = 3或4或5或6或7,
所以共有五种购买方案,分别为
方案一:购买A型3辆,B型7辆;
方案二:购买A型4辆,B型6辆;
方案三:购买A型5辆,B型5辆;
方案四:购买A型6辆,B型4辆;
方案五:购买A型7辆,B型3辆。
设总费用为W元,则W = 120m + 170(10 - m),即W = - 50m + 1700(3≤m≤7, 且m为正整数)。
∵W随m的增大而减小,
∴当购买A型7辆,B型3辆时,费用最少,
最少费用为 - 50×7 + 1700 = 1350(万元)。
答:该公司有五种购车方案。当购买A型7辆,B型3辆时,费用最少,最少费用为1350万元。

24. (12分)在$□ABCD$中,BE平分$∠ABC$交AD于点E。
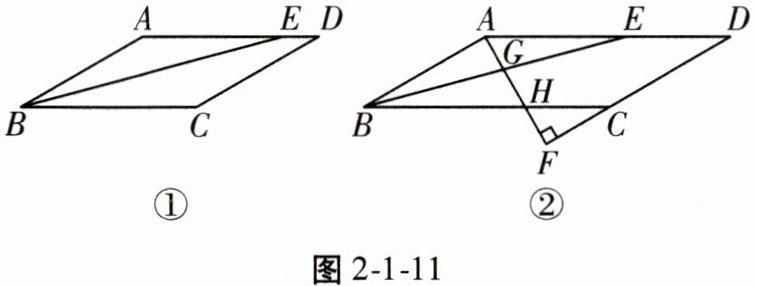
(1)如图2-1-11①,若$∠D= 30^{\circ },AB= \sqrt {6}$,求$△ABE$的面积;
(2)如图2-1-11②,过点A作$AF⊥DC$,交DC的延长线于点F,分别交BE,BC于点G,H,且$AB= AF$。求证:$ED-AG= FC$。

答案：

(1) 解:作BO⊥AD,垂足为点O,如图①。
∵四边形ABCD是平行四边形,
∴AD//BC,AB//CD,AB = CD,∠ABC = ∠D = 30°,
∴∠AEB = ∠CBE,∠BAO = ∠D = 30°,
∴BO = $\frac{1}{2}$AB = $\frac{\sqrt{6}}{2}$。
∵BE平分∠ABC,
∴∠ABE = ∠CBE,
∴∠ABE = ∠AEB,
∴AE = AB = $\sqrt{6}$,
∴△ABE的面积 = $\frac{1}{2}$AE×BO = $\frac{1}{2} \times \sqrt{6} \times \frac{\sqrt{6}}{2} = \frac{3}{2}$。

(2) 证明:过A作AN⊥BE交DC的延长线于点N,交BE于点Q,交BC于点P,如图②。
∵AB//CD,
∴∠BAQ = ∠ANF。
∵∠BAQ + ∠GAQ = ∠BGA + ∠GAQ = 90°,
∴∠BAQ = ∠BGA = ∠ANF。
又
∵∠BAG = ∠AFN = 90°,AB = AF,
∴△ABG≌△FAN,
∴AG = FN,
∴AG + FC = FN + FC = CN。
由
(1)得:AB = AE。
∵AN⊥BE,
∴∠BAP = ∠DAP。
∵AD//BC,
∴∠DAP = ∠BPA,
∴∠BAP = ∠BPA,
∴AB = PB = AE。
同理CP = CN。
∵AD = BC,
∴ED = CP = CN,
∴ED = AG + FC,
∴ED - AG = FC。