2025年实验班提优训练暑假衔接版七升八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版七升八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 图中以AB为边的三角形的个数是(
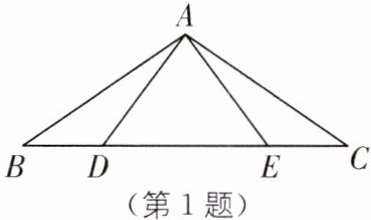
A.4
B.3
C.2
D.1
B
)。
A.4
B.3
C.2
D.1
答案:
B
2. 若线段AM,AN分别是△ABC的边BC上的高线和中线,则(
A.$ AM > AN $
B.$ AM \geq AN $
C.$ AM < AN $
D.$ AM \leq AN $
D
)。A.$ AM > AN $
B.$ AM \geq AN $
C.$ AM < AN $
D.$ AM \leq AN $
答案:
D
3. 如图,在△ABC中,$ AB = 7 $,$ AC = 5 $,AD是△ABC的中线,则△ABD与△ADC的周长之差为(
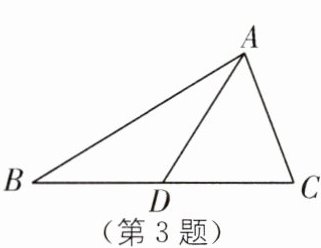
A.0
B.1
C.2
D.3
C
)。
A.0
B.1
C.2
D.3
答案:
C
4. 如图,AD,AE,AF分别是△ABC的中线、角平分线、高,下列各式中错误的是(
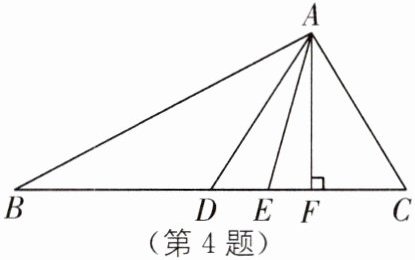
A.$ BC = 2CD $
B.$ \angle BAE = \frac{1}{2}\angle BAC $
C.$ \angle AFB = 90^{\circ} $
D.$ AE = CE $
D
)。
A.$ BC = 2CD $
B.$ \angle BAE = \frac{1}{2}\angle BAC $
C.$ \angle AFB = 90^{\circ} $
D.$ AE = CE $
答案:
D [解析]
∵AD,AE,AF 分别是△ABC 的中线、角平分线、高,
∴BC=2BD=2DC,∠BAE=∠CAE=$\frac{1}{2}$∠BAC,
∠AFB=∠AFC=90°。
故选项 A,B,C 正确,选项 D 错误。故选 D。
∵AD,AE,AF 分别是△ABC 的中线、角平分线、高,
∴BC=2BD=2DC,∠BAE=∠CAE=$\frac{1}{2}$∠BAC,
∠AFB=∠AFC=90°。
故选项 A,B,C 正确,选项 D 错误。故选 D。
5. 如图(1)所示,将长为6的长方形纸片沿虚线折成3个矩形,其中左右两侧长方形的宽相等,若要将其围成如图(2)所示的三棱柱形物体,则图中a的值可以是(
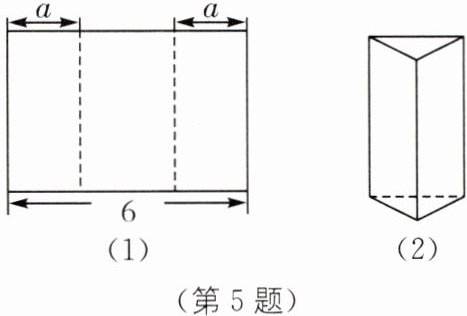
A.1
B.2
C.3
D.4
B
)。
A.1
B.2
C.3
D.4
答案:
B [解析]长为 6 的线段围成等腰三角形的腰长为 a,则底边长为 6 - 2a。
由题意,得 2a>6 - 2a,且 6 - 2a>0,
解得$\frac{3}{2}$<a<3,故 a=2。故选 B。
由题意,得 2a>6 - 2a,且 6 - 2a>0,
解得$\frac{3}{2}$<a<3,故 a=2。故选 B。
6. 已知a,b,c为△ABC的三边,化简$ |a - b - c| - |a + b - c| + 2a $的结果是
2c
。
答案:
2c
7. 新情境 数学与生活融合 木工师傅做木质长方形门框时,常常需要在其相邻两边钉上一根木条,这样做的目的是
固定
,其中所涉及的数学道理是三角形具有稳定性
。
答案:
固定 三角形具有稳定性
8. 下列各组数:①2,3,4;②2,3,5;③2,3,7;④3,3,3,其中能作为三角形的三边长的是
①④
(填写所有符合题意的序号)。
答案:
①④
9. 如果将长度分别为$ a - 2 $,$ a + 5 $和$ a + 2 $的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是
a>5
。
答案:
a>5
10. 中考新考法 新定义问题 若三边均不相等的三角形三边a,b,c满足$ a - b > b - c $(a为最长边,c为最短边),则称它为“不均衡三角形”。例如,一个三角形三边分别为7,5,4,因为$ 7 - 5 > 5 - 4 $,所以这个三角形为“不均衡三角形”。已知“不均衡三角形”三边分别为$ 2x + 2 $,16,$ 2x - 6 $,直接写出x的整数值为
10 或 12 或 13 或 14
。
答案:
10 或 12 或 13 或 14
11. 已知一等腰三角形的三边长分别为$ 3x - 2 $,$ 2x - 1 $,$ x + 3 $,试求这个等腰三角形的周长。
答案:
∵等腰三角形的三边长分别是 3x - 2,
2x - 1,x + 3,
①若 3x - 2=2x - 1,则 x=1,三边长为 1,1,4,1 + 1<4,不能组成三角形,舍去;
②若 2x - 1=x + 3,则 x=4,三边长为 7,7,10,周长为 24;
③若 3x - 2=x + 3,则 x=$\frac{5}{2}$,三边长为$\frac{11}{2}$,$\frac{11}{2}$,4,周长为 15。综上所述,它的周长是 24 或 15。
∵等腰三角形的三边长分别是 3x - 2,
2x - 1,x + 3,
①若 3x - 2=2x - 1,则 x=1,三边长为 1,1,4,1 + 1<4,不能组成三角形,舍去;
②若 2x - 1=x + 3,则 x=4,三边长为 7,7,10,周长为 24;
③若 3x - 2=x + 3,则 x=$\frac{5}{2}$,三边长为$\frac{11}{2}$,$\frac{11}{2}$,4,周长为 15。综上所述,它的周长是 24 或 15。
查看更多完整答案,请扫码查看


