《2025年实验班提优训练暑假衔接版七升八年级数学人教版》

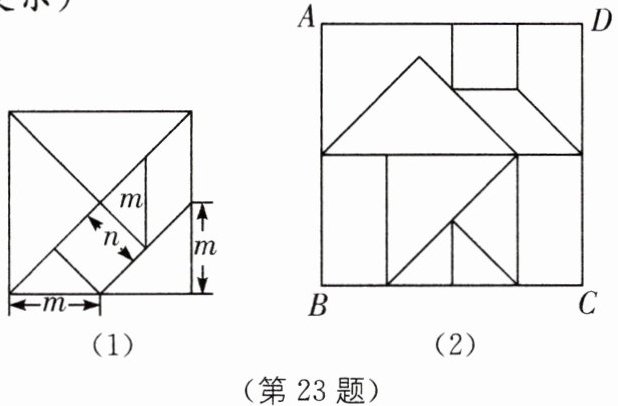
23. 传统文化 七巧板 七巧板(如图(1))是中国古代人民发明的一种传统智力玩具,它由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成(已知线段长度如图所示). 现将它拼成一个“房子”造型(如图(2)),恰好放入长方形$ABCD$容器中,求长方形容器的周长. (用含$m,n$的代数式表示)

答案： 由图可知：大等腰直角三角形的斜边长为$2m$，较大等腰直角三角形的斜边长为$2n$，平行四边形的短边长为$n$，正方形的边长为$n$，小等腰直角三角形的直角边长为$n$，
$\therefore BC = 2m + n$，$AB = 2n + n + n = 4n$，
$\therefore$ 长方形容器的周长为$2(AB + BC)=2(2m + n + 4n)=4m + 10n$。

24. $x$表示一个两位数,$y$表示一个三位数,若把$x放在y$的左边组成一个五位数,记为$A$,把$y放在x的左边组成一个五位数记为B$.
(1)用含$x,y的式子表示A-B$.
(2)$A-B$是 9 的倍数吗？为什么？

答案：
(1) $A = 1000x + y$，$B = 100y + x$。
$A - B=(1000x + y)-(100y + x)$
$=1000x + y - 100y - x = 999x - 99y$。
(2) $A - B$是$9$的倍数。理由如下：
因为$999x - 99y = 9(111x - 11y)$，
所以$A - B$是$9$的倍数。

25. 中考新考法 改变条件探究 学习了整式的加减运算后,老师给同学们布置了一道课堂练习题“当$a= -2,b= 2025$时,求$(3a^{2}b-2ab^{2}+4a)-2(2a^{2}b-3a)+2(ab^{2}+\frac {1}{2}a^{2}b)-1$的值”. 小盈做完后对同桌说：“老师给的条件$b= 2025$是多余的,这道题不给$b$的值,照样可以求出结果来.”同桌不相信她的话,亲爱的同学们,你相信小盈的说法吗？说说你的理由.

答案： 原式$=3a^{2}b - 2ab^{2}+4a - 4a^{2}b + 6a + 2ab^{2}+a^{2}b - 1 = 10a - 1$，
当$a = -2$时，原式$=-21$，
化简结果中不含字母$b$，即最后的结果与$b$的取值无关，$b = 2025$这个条件是多余的，
故小盈的说法是正确的。

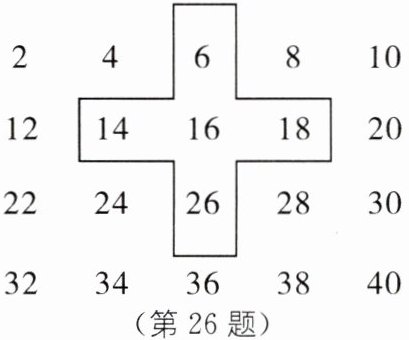
26. 将连续的偶数$2,4,6,8,…$排成下图：
(1)十字框中的五个数的和与中间的数 16 有什么关系？
(2)设中间的数为$x$,用整式表示十字框中的五个数的和.
(3)若将十字框上下左右移动,可框住另外的五个数,则这 5 个数的和能等于 920 吗？如能,写出这五个数；如不能,说明理由.

答案：
(1) 十字框中的五个数的和为$6 + 14 + 16 + 18 + 26 = 80 = 16×5$，即是$16$的$5$倍。
(2) 设中间的数为$x$，则十字框中的五个数的和为$(x - 10)+(x + 10)+(x - 2)+(x + 2)+x = 5x$，
所以五个数的和为$5x$。
(3) 能。理由如下：假设能够框出满足条件的五个数，设中间的数为$a$，
由
(2)，得$5a = 920$，所以$a = 184$。
因为$184 - 10 = 174$，$184 + 10 = 194$，$184 - 2 = 182$，$184 + 2 = 186$，
所以能框住五个数，使它们的和等于$920$。这五个数分别为$174$，$194$，$182$，$184$，$186$。