《2025年实验班提优训练暑假衔接版七升八年级数学人教版》

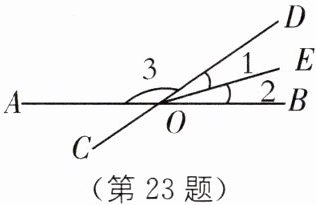
23. 如图,直线$AB与CD相交于点O$,$OE平分\angle BOD$,$\angle 3:\angle 2 = 8:1$,求$\angle AOC$的度数.

答案： 解：设∠2 = x，
∵OE平分∠BOD，
∴∠1 = ∠2 = x，
∵∠3:∠2 = 8:1，
∴∠3 = 8x，
∵∠1 + ∠2 + ∠3 = 180°，
∴x + x + 8x = 180°，
解得x = 18°，
∴∠BOD = ∠1 + ∠2 = 2x = 36°，
∵∠AOC与∠BOD是对顶角，
∴∠AOC = ∠BOD = 36°．
答：∠AOC的度数为36°．

24. 新情境构建方程模型解决实际问题某牛奶厂现有安全鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元；若制成酸奶销售,每吨可获取利润1200元；若制成奶片销售,每吨可获取利润2000元. 该工厂的生产能力是如果制成酸奶,每天可加工3吨；制成奶片,每天可加工1吨. 受人员限制,两种加工方式不可同时进行；受气温限制,这批牛奶必须4天内全部销售或加工完毕,为此该厂设计了两种方案：
方案一：尽可能地制成奶片,其余的直接销售鲜奶；
方案二：将一部分制成奶片,其余的制成酸奶销售,并恰好4天完成.
你认为选择哪种方案获利最多？

答案： 选择方案二获利最多. 理由如下：
方案一：制 4 天奶片共 4 吨，利润为 8000 元，则剩余 5 吨鲜奶，利润为 2500 元，所以总利润为 10500 元；
方案二：设加工了 $x$ 天奶片，列方程得 $x + 3(4 - x) = 9$，解得 $x = 1.5$，则奶片利润为 3000 元，酸奶利润为 9000 元，所以总利润为 12000 元，所以应选择方案二.

25. 如图,$A$,$B$,$C$是一条公路上的3个村庄,$A$,$B间的路程为100\mathrm{km}$,$A$,$C间的路程为40\mathrm{km}$,要在$A$,$B之间设一个车站P$,设$P$,$C之间的路程为x\mathrm{km}$.
(1)用含$x$的代数式表示车站到3个村庄的路程之和.
(2)若车站到3个村庄的路程之和为$102\mathrm{km}$,问车站应设在何处？
(3)若要使车站到3个村庄的路程总和最小,问车站应设在何处？

答案：

(1) 点 P 应分两种情况考虑.
①如图
(1)，点 P 在 A，C 之间，
$PC = x\mathrm{km}$，则 $PA = (40 - x)\mathrm{km}$，$PB = (60 + x)\mathrm{km}$.
所以 $PA + PB + PC = x + 40 - x + 60 + x = (100 + x)\mathrm{km}$.

②如图
(2)，点 P 在 B，C 之间，
$PC = x\mathrm{km}$，则 $PB = (60 - x)\mathrm{km}$，$PA = (40 + x)\mathrm{km}$.
所以 $PA + PB + PC = x + 60 - x + 40 + x = (100 + x)\mathrm{km}$.
故车站到 3 个村庄的路程之和为 $(100 + x)\mathrm{km}$.
(2) 依题意，得 $100 + x = 102$，解得 $x = 2$.
故车站应设在 C 村庄的左边或右边 $2\mathrm{km}$ 处.
(3) 要使车站到三个村庄的路程之和最小，即 $100 + x$ 最小，则当 $x = 0$ 时，$100 + x$ 的值最小，即车站应设在 C 村庄处.