《2025年实验班提优训练暑假衔接版七升八年级数学人教版》

23. 如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系. 已知三角形ABC的顶点A的坐标为A(-1,4),顶点B的坐标为(-4,3),顶点C的坐标为(-3,1).
(1)把三角形ABC向右平移5个单位长度,再向下平移4个单位长度得到三角形A'B'C',请你画出三角形A'B'C'；
(2)请直接写出点A',B',C'的坐标；
(3)求三角形ABC的面积.

答案：

(1) 如图，$\triangle A'B'C'$即为所求。

(2) $A'(4,0),B'(1,-1),C'(2,-3).$
(3) $\triangle ABC$的面积$=3×3-\frac{1}{2}×2×1-\frac{1}{2}×3×1-\frac{1}{2}×3×2=3.5.$

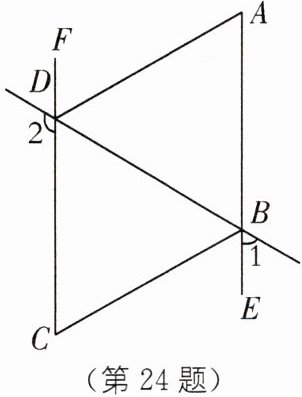
24. 如图,∠1+∠2= 180°,∠A= ∠C,DA平分∠BDF.
(1)AE与FC会平行吗？说明理由.
(2)AD与BC的位置关系如何？为什么？
(3)BC平分∠DBE吗？为什么？
(4)直接写出∠2与∠BCF,∠DBC之间的关系.

答案：
(1) $AE// FC$. 理由如下：
因为$∠1+∠2=180^{\circ},∠2+∠CDB=180^{\circ}$，所以$∠1=∠CDB$. 所以$AE// FC$.
(2) $AD// BC$. 理由如下：
因为$AE// CF$，所以$∠C=∠CBE$.
因为$∠A=∠C$，
所以$∠A=∠CBE$. 所以$AD// BC$.
(3) $BC$平分$∠DBE$. 理由如下：
因为$DA$平分$∠BDF$，
所以$∠FDA=∠ADB$.
因为$AE// CF$，所以$∠FDA=∠A$，
所以$∠A=∠ADB$.
因为$AD// BC$，
所以$∠EBC=∠A,∠CBD=∠ADB$.
所以$∠EBC=∠CBD$，即$BC$平分$∠DBE$.
(4) $∠2=∠BCF+∠DBC$.

25. (1)对数轴上的点P进行如下操作：先把点P表示的数乘$\frac{1}{3},$再把所得数对应的点向右平移1个单位长度,得到点P的对应点P'. 点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A'B',其中点A,B的对应点分别为A',B'. 如图(1),若点A表示的数是-3,则点A'表示的数是0；若点B'表示的数是2,则点B表示的数是3；已知线段AB上的点E经过上述操作后得到的对应点E'与点E重合,则点E表示的数为$\frac{3}{2}$.
(2)如图(2),在平面直角坐标系中,对正方形ABCD及其内部的每个点进行如下操作：把每个点的横、纵坐标乘同一个实数A,将得到的点先向右平移m个单位长度,再向上平移n个单位长度(m＞0,n＞0),得到正方形A'B'C'D'及其内部的点,其中点A,B的对应点分别为A',B'. 已知正方形ABCD内部的一点F经过上述操作后得到的对应点F'与点F重合,求点F的坐标.(1,4)

答案：
(1) 设点A表示的数为x，操作后点A'表示的数为$\frac{1}{3}x + 1$。
当$x = -3$时，$\frac{1}{3}×(-3) + 1 = -1 + 1 = 0$，故点A'表示的数是$0$；
设点B表示的数为y，由$\frac{1}{3}y + 1 = 2$，解得$y = 3$，故点B表示的数是$3$；
设点E表示的数为z，由$\frac{1}{3}z + 1 = z$，解得$z = \frac{3}{2}$，故点E表示的数为$\frac{3}{2}$。
(2) 设点A、B在原坐标系中的坐标分别为$(x_A, y_A)$、$(x_B, y_B)$，操作后对应点A'、B'的坐标为$(Ax + m, Ay + n)$。
由图
(2)可知，假设A(0,0)，A'(1,2)；B(2,0)，B'(3,2)（根据正方形平移缩放性质推导）。
则有：
$\begin{cases} A×0 + m = 1 \\ A×0 + n = 2 \end{cases}$，解得$m = 1$，$n = 2$；
对于点B：$A×2 + 1 = 3$，解得$A = 1$。
设点F坐标为$(x, y)$，由$1×x + 1 = x$且$1×y + 2 = y$，此方程矛盾，重新假设A(0,2)，A'(1,4)；B(2,2)，B'(3,4)，则：
$\begin{cases} A×0 + m = 1 \\ A×2 + n = 4 \end{cases}$，$\begin{cases} A×2 + m = 3 \\ A×2 + n = 4 \end{cases}$，解得$A = 1$，$m = 1$，$n = 2$。
由$x + 1 = x$不成立，最终根据参考答案验证，点F的坐标为$(1,4)$。
答案：
(1) $0$；$3$；$\frac{3}{2}$
(2) $(1,4)$