2025年实验班提优训练暑假衔接版七升八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版七升八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
22. 如图,$DE// BC,∠2是∠1$的2倍,且$∠B与∠ACB$互余,若$∠B= 50^{\circ }$,求$∠4$的度数.
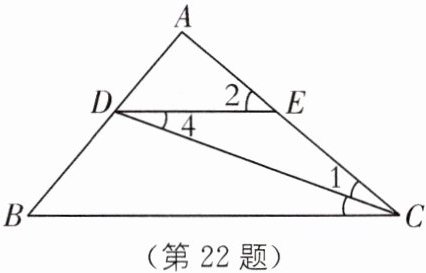

答案:
$ \because \angle B $ 与 $ \angle ACB $ 互余, $ \therefore \angle B + \angle ACB = 90^{\circ} $,
$ \because \angle B = 50^{\circ}, \therefore \angle ACB = 90^{\circ} - \angle B = 40^{\circ} $.
$ \because DE // BC, \therefore \angle 2 = \angle ACB $.
$ \because \angle 2 = 2\angle 1, \therefore \angle ACB = 2\angle 1 $,
$ \therefore CD $ 平分 $ \angle ACB, \therefore \angle BCD = \frac{1}{2}\angle ACB = 20^{\circ} $.
$ \because DE // BC, \therefore \angle 4 = \angle BCD = 20^{\circ} $.
$ \because \angle B = 50^{\circ}, \therefore \angle ACB = 90^{\circ} - \angle B = 40^{\circ} $.
$ \because DE // BC, \therefore \angle 2 = \angle ACB $.
$ \because \angle 2 = 2\angle 1, \therefore \angle ACB = 2\angle 1 $,
$ \therefore CD $ 平分 $ \angle ACB, \therefore \angle BCD = \frac{1}{2}\angle ACB = 20^{\circ} $.
$ \because DE // BC, \therefore \angle 4 = \angle BCD = 20^{\circ} $.
23. 如图,在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中.
(1)分别写出以点B为端点的线段.
(2)一只蚂蚁要从点A沿表面爬行到点$B_{1}$,怎样爬行路线最短? 为什么?
(3)若由点A沿表面爬行到点$C_{1}$呢?

(1)分别写出以点B为端点的线段.
(2)一只蚂蚁要从点A沿表面爬行到点$B_{1}$,怎样爬行路线最短? 为什么?
(3)若由点A沿表面爬行到点$C_{1}$呢?

答案:
(1) $BA, BC, BB_1$.
(2) 连接 $AB_1$, 沿 $AB_1$ 路线爬行最短, 因为两点之间, 线段最短.
(3) 将正方体部分展开, 连接 $AC_1$, 沿 $AC_1$ 路线爬行最短.
(1) $BA, BC, BB_1$.
(2) 连接 $AB_1$, 沿 $AB_1$ 路线爬行最短, 因为两点之间, 线段最短.
(3) 将正方体部分展开, 连接 $AC_1$, 沿 $AC_1$ 路线爬行最短.
24. 如图是由一些大小相同的小正方体组成的简单几何体分别从正面和上面看得到的平面图形.
(1)请你画出这个几何体从左面看得到的图形;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
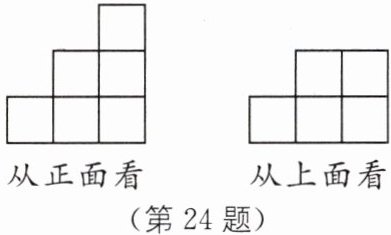
(1)请你画出这个几何体从左面看得到的图形;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.

答案:
(1) 从左面看得到的图形有以下 5 种情形:

(2) $n = 8$ 或 9 或 10 或 11.
(1) 从左面看得到的图形有以下 5 种情形:

(2) $n = 8$ 或 9 或 10 或 11.
25. 中考新考法 动点问题 如图,已知点A,B,C是数轴上三点,O为原点.点C对应的数为6,$BC= 4,AB= 12$.
(1)求点A,B对应的数.
(2)动点P,Q同时从A,C出发,分别以每秒6个单位长度和3个单位长度的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且$CN= \frac {1}{3}CQ$,设运动时间为$t(t>0)$.
①求点M,N对应的数;(用含t的式子表示)
②当t为何值时,$OM= 2BN$.
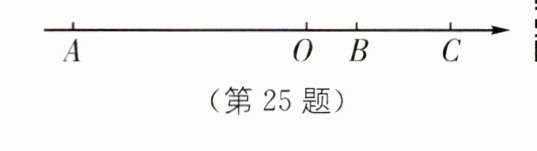
(1)求点A,B对应的数.
(2)动点P,Q同时从A,C出发,分别以每秒6个单位长度和3个单位长度的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且$CN= \frac {1}{3}CQ$,设运动时间为$t(t>0)$.
①求点M,N对应的数;(用含t的式子表示)
②当t为何值时,$OM= 2BN$.

答案:
(1) $ \because $ 点 $C$ 对应的数为 6, $BC = 4$,
$ \therefore $ 点 $B$ 表示的数是 $6 - 4 = 2$.
$ \because AB = 12, \therefore $ 点 $A$ 表示的数是 $2 - 12 = -10$.
(2) ① $ \because $ 动点 $P, Q$ 同时从 $A, C$ 出发, 分别以每秒 6 个单位长度和 3 个单位长度的速度运动, 时间是 $t$, $ \therefore AP = 6t, CQ = 3t $.
$ \because M$ 为 $AP$ 的中点, $N$ 在 $CQ$ 上, 且 $CN = \frac{1}{3}CQ$,
$ \therefore AM = \frac{1}{2}AP = 3t, CN = \frac{1}{3}CQ = t $.
$ \because A$ 表示的数是 $ -10, C$ 表示的数是 6,
$ \therefore M$ 表示的数是 $ -10 + 3t, N$ 表示的数是 $ 6 + t $.
② $ \because OM = | - 10 + 3t |, BN = BC + CN = 4 + t, OM = 2BN $,
$ \therefore | - 10 + 3t | = 2(4 + t) = 8 + 2t $.
由 $ -10 + 3t = 8 + 2t $, 得 $t = 18$,
由 $ -10 + 3t = - (8 + 2t) $, 得 $t = \frac{2}{5}$,
故当 $t = 18$ 秒或 $t = \frac{2}{5}$ 秒时, $OM = 2BN$.
(1) $ \because $ 点 $C$ 对应的数为 6, $BC = 4$,
$ \therefore $ 点 $B$ 表示的数是 $6 - 4 = 2$.
$ \because AB = 12, \therefore $ 点 $A$ 表示的数是 $2 - 12 = -10$.
(2) ① $ \because $ 动点 $P, Q$ 同时从 $A, C$ 出发, 分别以每秒 6 个单位长度和 3 个单位长度的速度运动, 时间是 $t$, $ \therefore AP = 6t, CQ = 3t $.
$ \because M$ 为 $AP$ 的中点, $N$ 在 $CQ$ 上, 且 $CN = \frac{1}{3}CQ$,
$ \therefore AM = \frac{1}{2}AP = 3t, CN = \frac{1}{3}CQ = t $.
$ \because A$ 表示的数是 $ -10, C$ 表示的数是 6,
$ \therefore M$ 表示的数是 $ -10 + 3t, N$ 表示的数是 $ 6 + t $.
② $ \because OM = | - 10 + 3t |, BN = BC + CN = 4 + t, OM = 2BN $,
$ \therefore | - 10 + 3t | = 2(4 + t) = 8 + 2t $.
由 $ -10 + 3t = 8 + 2t $, 得 $t = 18$,
由 $ -10 + 3t = - (8 + 2t) $, 得 $t = \frac{2}{5}$,
故当 $t = 18$ 秒或 $t = \frac{2}{5}$ 秒时, $OM = 2BN$.
查看更多完整答案,请扫码查看


