《2025年系统集成暑假生活北京师范大学出版社八年级数学》

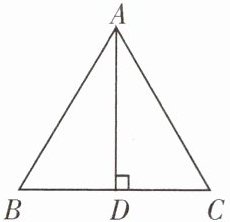
9. 如图,在 $ \triangle ABC $ 中,$ AD \perp BC $,垂足为 $ D $,需增加一个条件:____,可得 $ \mathrm{Rt} \triangle ABD \cong \mathrm{Rt} \triangle ACD $.

答案： $ BD = DC $ (答案不唯一)

10. 如果两个直角三角形的____分别对应相等,那么这两个直角三角形全等.

答案： 两条直角边(答案不唯一)

11. 如图,点 $ B $,$ F $,$ C $,$ E $ 在同一直线上,$ BF = CE $,$ AB \perp BE $,$ DE \perp BE $,垂足分别为 $ B $,$ E $ 且 $ AB = DE $,连接 $ AC $,$ DF $.
求证:$ \angle A = \angle D $.

答案： 提示:根据已知利用 SAS 判定 $ \triangle ABC \cong \triangle DEF $,又全等三角形的对应角相等,从而得到 $ \angle A = \angle D $.

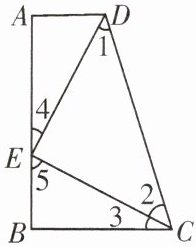
12. 如图,$ \angle A = \angle B = 90^{\circ} $,$ E $ 是 $ AB $ 上的一点,且 $ AE = BC $,$ \angle 1 = \angle 2 $.
(1)$ \mathrm{Rt} \triangle ADE $ 与 $ \mathrm{Rt} \triangle BEC $ 全等吗? 并说明理由.
(2)$ \triangle CDE $ 是不是直角三角形? 并说明理由.

答案： 提示:
(1)根据 $ \angle 1 = \angle 2 $,得 $ DE = CE $,利用“HL”可证明 $ Rt\triangle ADE \cong Rt\triangle BEC $;
(2)$ \triangle CDE $ 是直角三角形,由 $ Rt\triangle ADE \cong Rt\triangle BEC $ 得,$ \angle 3 = \angle 4 $,从而得 $ \angle 4 + \angle 5 = 90^{\circ} $,则 $ \angle DEC = 90^{\circ} $,即 $ \triangle CDE $ 是直角三角形.