11. 已知$a$,$b$,$c为\triangle ABC$的三边长,且满足$a^{2}c^{2}-b^{2}c^{2}= a^{4}-b^{4}$,试判断$\triangle ABC$的形状。
答案:
等腰三角形或直角三角形
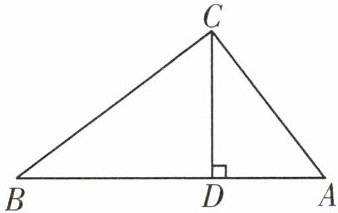
12. 如图,在$\triangle ABC$中,$CD是AB$边上的高,且$CD^{2}= AD\cdot BD$。求证:$\triangle ABC$是直角三角形。

答案:
证明:因为 CD 为 AB 边上的高,
所以在 $Rt\triangle ACD$ 和 $Rt\triangle BCD$ 中,
$CD^{2}+BD^{2}=BC^{2}$, ①
$CD^{2}+AD^{2}=AC^{2}$. ②
又 $CD^{2}=AD\cdot BD$, ③
联立①②③可得 $(AD+BD)^{2}=BC^{2}+AC^{2}=AB^{2}$,
所以 $\triangle ABC$ 是直角三角形.
![img alt=13]
所以在 $Rt\triangle ACD$ 和 $Rt\triangle BCD$ 中,
$CD^{2}+BD^{2}=BC^{2}$, ①
$CD^{2}+AD^{2}=AC^{2}$. ②
又 $CD^{2}=AD\cdot BD$, ③
联立①②③可得 $(AD+BD)^{2}=BC^{2}+AC^{2}=AB^{2}$,
所以 $\triangle ABC$ 是直角三角形.
![img alt=13]
查看更多完整答案,请扫码查看


