10. 三角形的三条中位线长分别是 $3\mathrm{cm}$,$4\mathrm{cm}$,$5\mathrm{cm}$,则这个三角形的周长为______。
答案:
24 cm
11. $E$ 点为正方形 $ABCD$ 的对角线 $AC$ 上一点,且 $AE = AB$,连接 $BE$,则 $\angle CBE = $______。
答案:
$22.5^{\circ}$
12. 求证:顺次连接矩形各边中点的四边形是菱形。
答案:
通过连接矩形的对角线,利用三角形中位线定理得出顺次连接矩形各边中点所形成的四边形的四条边都相等,根据菱形的定义,可证明顺次连接矩形各边中点的四边形是菱形。
13. 如图,在四边形 $ABCD$ 中,$AD// BC$,$AB = DC = AD$,$\angle C = 60^{\circ}$,$AE\perp BD$ 于点 $E$,$F$ 是 $CD$ 的中点,连接 $EF$。
求证:四边形 $AEFD$ 是平行四边形。
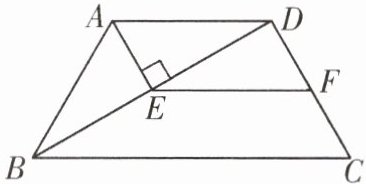
求证:四边形 $AEFD$ 是平行四边形。

答案:
一组对边平行且相等的四边形是平行四边形,因为$EF// AD$且$EF = AD$,所以四边形$AEFD$是平行四边形。
14. 如图,$P$ 是正方形 $ABCD$ 内一点,在正方形 $ABCD$ 外有一点 $E$,满足 $\angle ABE = \angle CBP$,$BE = BP$。
求证:(1)$\triangle CPB\cong\triangle AEB$;
(2)$PB\perp BE$。
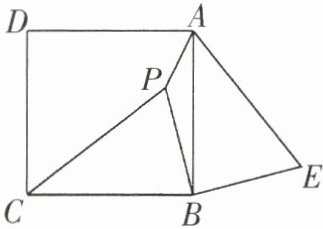
求证:(1)$\triangle CPB\cong\triangle AEB$;
(2)$PB\perp BE$。

答案:
(1) 因为四边形$ABCD$是正方形,所以$BC = AB$。在$\triangle CPB$和$\triangle AEB$中,$\left\{\begin{array}{l}BC = AB\\\angle CBP=\angle ABE\\BP = BE\end{array}\right.$,由$SAS$可得$\triangle CPB\cong\triangle AEB$。
(2) 因为$\angle ABC = 90^{\circ}$,即$\angle CBP+\angle PBA=90^{\circ}$,又$\angle ABE=\angle CBP$,所以$\angle ABE+\angle PBA = 90^{\circ}$,即$\angle PBE = 90^{\circ}$,所以$PB\perp BE$。
综上,
(1) 得证$\triangle CPB\cong\triangle AEB$;
(2) 得证$PB\perp BE$。
(1) 因为四边形$ABCD$是正方形,所以$BC = AB$。在$\triangle CPB$和$\triangle AEB$中,$\left\{\begin{array}{l}BC = AB\\\angle CBP=\angle ABE\\BP = BE\end{array}\right.$,由$SAS$可得$\triangle CPB\cong\triangle AEB$。
(2) 因为$\angle ABC = 90^{\circ}$,即$\angle CBP+\angle PBA=90^{\circ}$,又$\angle ABE=\angle CBP$,所以$\angle ABE+\angle PBA = 90^{\circ}$,即$\angle PBE = 90^{\circ}$,所以$PB\perp BE$。
综上,
(1) 得证$\triangle CPB\cong\triangle AEB$;
(2) 得证$PB\perp BE$。
查看更多完整答案,请扫码查看


